Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Ta có qua diện tích giới hạn bởi khung dây:
Suy ra bán kính vòng dây:
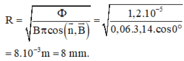
Ta có qua diện tích giới hạn bởi khung dây:
\(\Phi=BScos\left(\overrightarrow{n},\overrightarrow{B}\right)=B\pi R^2cos\left(\overrightarrow{n},\overrightarrow{B}\right)\)
Suy ra bán kính vòng dây:
\(R=\sqrt{\dfrac{\Phi}{B\pi cos\left(\overrightarrow{n},\overrightarrow{B}\right)}}=\sqrt{\dfrac{1,2.10^{-5}}{0,06.3,14.cos0^o}}\)
\(=8.10^{-3}m=8mm\)
Ta có: ϕ = BScos( n , ⇀ B ⇀ ) = BπR 2 cos( n , ⇀ B ⇀ )
=> R = ϕ Bπcos ( n ⇀ , B ⇀ ) = 8 . 10 - 3 m = 8 mm.
Đáp án D
+ F = BScosa
® 
=
2
.
10
-
4
m
2
® R » 8. 10 - 3 m = 8 mm.
\(\Phi=BScos\alpha=0,25.25cos30=\dfrac{25\sqrt{3}}{8}\\ e_e=-\dfrac{\Delta\Phi}{\Delta t}=-\dfrac{0,2}{0,05}=-4\)
\(e_c\) có trị tuyệt đối và đơn vị của \(\phi\) là Wb và đơn vị của \(e_c\) là V nhé
Đáp án B