Tìm tất cả các giá trị thực của tham số m để cặp phương trình sau tương đương:
m x 2 - 2 m - 1 x + m - 2 = 0 1 và m - 2 x 2 - 3 x + m 2 - 15 = 0 2
A. m = −5.
B. m = −5; m = 4.
C. m = 4.
D. m = 5.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

- Ta có (2) ⇔ x + 2 2 x 2 + m x - 2 = 0 ⇔ x = − 2 2 x 2 + m x − 2 = 0
Do hai phương trình tương đương nên x = −2 cũng là nghiệm của phương trình (1)
- Thay x = −2 vào (1), ta được 2 - 2 2 + m - 2 - 2 = 0 ⇔ m = 3.
- Với m = 3, ta có:
...(1) trở thành 2 x 2 + 3 x - 2 = 0 ⇔ x = - 2 hoặc x = 1 2
...(2) trở thành 2 x 3 + 7 x 2 + 4 x - 4 = 0 ⇔ x + 2 2 2 x + 1 = 0 ⇔ x = - 2 hoặc x = 1 2
Suy ra hai phương trình tương đương.
Vậy m = 3 thỏa mãn.
Đáp án cần chọn là: B

Đáp án B.
Đặt t = log2 x,
khi đó m + 1 log 2 2 x + 2 log 2 x + m - 2 = 0
⇔ m + 1 t 2 + 2 t + m - 2 = 0 (*).
Để phương trình (*) có hai nghiệm phân biệt
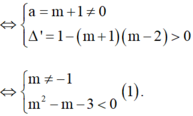
Khi đó gọi x1, x2 lần lượt hai nghiệm của phương trình (*).
Vì 0 < x1 < 1 < x2 suy ra
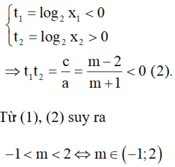
Ta có (1) ⇔ x - 1 m x - m + 2 = 0 ⇔ x = 1 m x − m + 2 = 0
Do hai phương trình tương đương nên x = 1 cũng là nghiệm của phương trình (2)
Thay x = 1 vào (2), ta được
m - 2 - 3 + m 2 - 15 = 0 ⇔ m 2 + m - 20 = 0 ⇔ m = − 5 m = 4
Với m = −5, ta có
(1) trở thành - 5 x 2 + 12 x - 7 = 0 ⇔ x = 7 5 hoặc x = 1
(2) trở thành - 7 x 2 - 3 x + 10 = 0 ⇔ x = - 10 7 hoặc x = 1
Suy ra hai phương trình không tương đương
Với m = 4, ta có
(1) trở thành 4 x 2 - 6 x + 2 = 0 ⇔ x = 1 2 hoặc x = 1
(2) trở thành 2 x 2 - 3 x + 1 = 0 ⇔ x = 1 2 hoặc x = 1
Suy ra hai phương trình tương đương.
Vậy m = 4 thỏa mãn.
Đáp án cần chọn là: C