Từ các chữ số của tập hợp A={0;1;2;3;4;5;6} lập được bao nhiêu số tự nhiên gồm 5 chữ số
A. 14406
B. 13353
C. 15223
D. 14422
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(A=\left\{15;65;51;61\right\}\)
b) \(B=\left\{105;501;156;165;561;516;615;651;510;150\right\}\)

Đáp án B

Khi đó
- Số cách chọn chữ số α có 5 cách chọn vì α ≠ 0 .
- Số cách chọn chữ số b có 5 cách chọn vì b ≠ α .
- Số cách chọn chữ số c có cách chọn vì c ≠ α và c ≠ b .
Do đó tập S có 5.5.4 = 100 phần tử.
Không gian mẫu là chọn ngẫu nhiên1 số từ tập S .
Suy ra số phần tử của không gian mẫu là Ω = C 100 1 = 100 .
Gọi X là biến cố "Số được chọn có chữ số cuối gấp đôi chữ số đầu". Khi đó ta có các bộ số là 1 b 2 hoặc 2 b 4 thỏa mãn biến cố X và cứ mỗi bộ thì b có 4 cách chọn nên có tất cả số thỏa yêu cầu.
Suy ra số phần tử của biến cố X là Ω X = 8 .
Vậy xác suất cần tính P ( X ) = Ω X Ω = 8 100 = 2 25 .

Giả sử a là chữ số hàng chục và b là chữ số hàng đơn vị của số cần tìm
Ta có:
Tập hợp A:
Số cần tìm là số có hai chữ số nên chữ số hàng chục a ≠ 0.
Vì a + b = 8 nên a chỉ có thể lấy các giá trị 1, 2, 3, 4, 5, 6, 7, 8.
Vậy, Tập hợp A = {17 ; 26 ; 35 ; 44 ; 53 ; 62 ; 71 ; 80}.
Tập hợp B:
Số cần tìm là số có hai chữ số nên chữ số hàng chục a ≠ 0.
Số cần tìm được tạo thành từ hai trong bốn số 0 ; 3 ; 5 ; 8
Vậy, Tập hợp B = {30 ; 35 ; 38 ; 50 ; 53 ; 58 ; 80 ; 83 ; 85}.

a) x-5=22 ⇒ x=27 (xϵN)
⇒ Tập hợp có 1 phần tử xϵN
b) 2.y.0=15 ⇒ y.0=15/2 ⇒ y không có phần tử (xϵN)
c) y.0=15 ⇒ y không có phần tử (xϵN)
d) f ϵ {0;5) ⇒ Tập hợp có 2 phần tử fϵN
e) e ϵ {1;2;4;6) ⇒ Tập hợp có 4 phần tử eϵN

có 1 phần tử
A={7}có 1 phần tử
B là tập hợp rỗng
D là tập hợp rỗng
có 1 phần tử
tập hợp A có 4 tập hợp con

ong số học, bội số chung nhỏ nhất (hay còn gọi tắt là bội chung nhỏ nhất, viết tắt là BCNN, tiếng Anh: least common multiple hoặc lowest common multiple (LCM) hoặc smallest common multiple) của hai số nguyên a và b là số nguyên dương nhỏ nhất chia hết cho cả a và b.[1] Tức là nó có thể chia cho a và b mà không để lại số dư. Nếu a hoặc b là 0, thì không tồn tại số nguyên dương chia hết cho a và b, khi đó quy ước rằng LCM(a, b) là 0.
Định nghĩa trên đôi khi được tổng quát hoá cho hơn hai số nguyên dương: Bội chung nhỏ nhất của a1,..., an là số nguyên dương nhỏ nhất là bội số của a1,..., an.
Gọi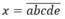
Để lập ta chọn các số a;b;c;d;e theo thứ tự sau:
Chọn a: Vi a ∈ A; a ≠ 0 nên ta có cách chọn a
Vì b ∈ A và b có thể trùng với a nên với mỗi cách chọn a ta có cách chọn b
Tương tự : với mỗi cách chọn a;b có cách chọn c
với mỗi cách chọn a;b;c có cách chọn d
với mỗi cách chọn a;b;c;d có cách chọn e
Vậy theo quy tắc nhân ta có: 6.7.7.7.7 = 14406 số thỏa yêu cầu bài toán.
Chọn A.