Cho hàm số y = 2 x + 3 x + 1 có đồ thị là (C) . Có bao nhiêu tiếp tuyến của đồ thị (C) tại những điểm thuộc đồ thị có khoảng cách đến đường thẳng d1: 3x+ 4y-2=0 bằng 2.
A. 2.
B. 3.
C. 4.
D. 0.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

- Giả sử ![]()
- Ta có 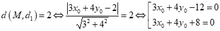
- Với 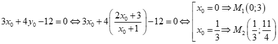
- Với 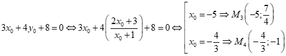
Suy ra có 4 tiếp tuyến.
Chọn C.

\(y'=\dfrac{-4}{\left(x-1\right)^2}\)
a) \(y'=-1\Rightarrow\left[{}\begin{matrix}x=3\\x=-1\end{matrix}\right.\)
pt tiếp tuyến : \(\left[{}\begin{matrix}y=-\left(x-3\right)+4=-x+7\\y=-\left(x+1\right)=-x-1\end{matrix}\right.\)
b) \(k=\pm1\)
\(y'< 0\forall x\Rightarrow y'=-1\)
làm như trên
c) hoành độ tiếp điểm \(x=\pm2\)
TH x = 2
\(k=-4\)
pt tiếp tuyến : \(y=-4\left(x-2\right)+6=-4x+14\)
TH x = -2
\(k=-\dfrac{4}{9}\)
pt tiếp tuyến : \(y=-\dfrac{4}{9}\left(x+2\right)+\dfrac{2}{3}=-\dfrac{4}{9}x-\dfrac{2}{9}\)

+ Hàm số đã cho có TCĐ là x=1 và TCN là y= 1 nên tâm đối xứng- là giao điểm của 2 đường tiệm cận có tọa độ là I (1; 1)
+ Ta có ![]()
Gọi 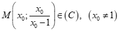
+ Phương trình tiếp tuyến tại M có dạng
![]()
![]()
+ 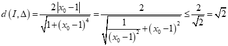
+ Dấu " = " xảy ra khi và chỉ khi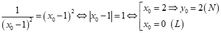
Tung độ này gần với giá trị ![]() nhất trong các đáp án.
nhất trong các đáp án.
Chọn D.

Đáp án D
Có f ' x = 3 x 2 − 12 x + 9 ; f '' x = 6 x − 12 .
Do đó 2 f ' x − x f '' x − 6 = 0 ⇔ 2 3 x 2 − 12 x + 9 − x 6 x − 12 − 6 = 0 ⇔ x = 1
Vậy tiếp tuyến có được tại điểm có tung độ là 1 tức là x 3 − 6 x 2 + 9 x + 1 = 1 ⇔ x = 0 x = 3
Có f ' 0 = 9 ≠ f ' 3 = − 9 vậy nên ta sẽ có 2 tiếp tuyến tại 2 điểm có hoành độ x = 0 ; x = 3 .

Đáp án D
có f ' x = 3 x 2 − 12 x + 9 ; f '' x = 6 x − 12 . Do đó
2 f ' x − x f '' x − 6 = 0 ⇔ 2 3 x 2 − 12 x + 9 − x 6 x − 12 − 6 = 0 ⇔ x = 1
Vậy tiếp tuyến có được tại điểm có tung độ là 1 tức là x 3 − 6 x 2 + 9 x + 1 = 1 ⇔ x = 0 x = 3
Có f ' 0 = 9 ≠ f ' 3 = − 9 vậy nên ta sẽ có 2 tiếp tuyến tại 2 điểm có hoành độ
x = 0 ; x = 3

Đáp án A.
Ta có f ' x = 3 x 2 - 12 x + 9 ⇒ f ' ' x = 6 x + 12 ; ∀ x ∈ ℝ .
Khi đó 2 f ' x - x . f ' ' x - 6 = 0 ⇔ 2 2 x 2 - 12 x + 9 - x 6 x - 12 - 6 = 0 ⇔ x = 1 .
Theo bài ra, ta có f x 0 = 1 ⇔ x 0 3 - 6 x 0 2 + 9 x 0 + 1 = 1 ⇒ [ x 0 = 0 x 0 = 3 .
Vậy có 2 tiếp tuyến của đồ thị hàm số (C) đi qua điểm có tung độ bằng 1.

Giao điểm của đồ thị hàm số (C) và trục tung là điểm N(0;1)
Ta có : \(f'\left(x\right)=\frac{3}{\left(1-x\right)^2}\) suy ra tiếp tuyến tại điểm N là \(\left(\Delta\right):y=3x+1\Leftrightarrow\left(\Delta\right):3x-y+1=0\)
Xét điểm \(M\left(a+1;\frac{2a+3}{-a}\right)\in\left(C\right),a>0\)
Ta có : \(d_{M\\Delta }=\frac{\left|3\left(a+1\right)+\frac{2a+3}{a}+1\right|}{\sqrt{10}}=\frac{1}{\sqrt{10}}.\frac{3a^2+6a}{+3a}=\frac{3}{\sqrt{10}}\left(a+\frac{2}{a}+1\right)\ge\frac{3}{\sqrt{10}}\left(2\sqrt{2}+1\right)\)
Dấu bằng xảy ra khi \(a=\frac{2}{a}\Leftrightarrow a=\sqrt{2}\Rightarrow M\left(\sqrt{2}+1;\frac{2\sqrt{2}+5}{-\sqrt{2}}\right)\)
+ Giả sử M( x 0 ; y 0 ) ∈ C suy ra y 0 = 2 x 0 + 3 x 0 + 1
+Ta có
Ta tìm được 4 điểm M suy ra có 4 tiếp tuyến.
Chọn C.