Cho tứ diện đều ABCD, M là trung điểm BC. Tính cosin của góc giữa hai đường thẳng AB và DM
A. 3 6
B. 2 2
C. 3 2
D. 1 2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
14 tháng 10 2019
Đúng(0)
Những câu hỏi liên quan
CM
8 tháng 3 2019
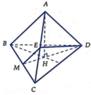
Đáp án A
Giả sử tứ diện đều cạnh a
Gọi H là tâm đường tròn ngoại tiếp Δ B C D ⇒ A H ⊥ B C D
Gọi E là trung điểm
A C ⇒ M E // A B ⇒ A B , D M = M E , M D
Ta có M E = a 2 , E D = M D = a 3 2
cos
A
B
,
D
M
=
cos
M
E
,
M
D
=
cos
E
M
D
⏜
cos
E
M
D
⏜
=
M
E
2
+
M
D
2
−
E
D
2
2
M
E
.
M
D
=
3
6
NM
1
NV
Nguyễn Việt Lâm
Giáo viên
1 tháng 3 2020
Gọi cạnh của tứ diện là a \(\Rightarrow\) tất cả các mặt bên đều là tam giác đều cạnh a
\(\Rightarrow CM=DM=\frac{a\sqrt{3}}{2}\) (trung tuyến tam giác đều)
\(\Rightarrow cos\widehat{CMD}=\frac{CM^2+DM^2-CD^2}{2CM.DM}=\frac{\frac{3a^2}{4}+\frac{3a^2}{4}-a^2}{2.\frac{3a^2}{4}}=\frac{1}{3}\)
CM
4 tháng 1 2020
Đáp án A
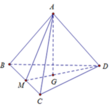
Giả sử cạnh tứ diện là a và G là trọng tâm tam giác BCD
Ta có A D ; D M ⏜ = A D M ⏜ và cos A D M ⏜ = G D A D = 3 3
A M ; D M ⏜ = A M G ⏜ , c o s A M G ⏜ = M G A M = 1 3
A B ; A M ⏜ = M A B ⏜ = 30 °
Sử dụng PP loại trừ