Tính cạnh huyền của một tam giác biết tỉ số các cạnh góc vuông 3:4 và chu vi tam giác bằng 36 cm
A. 9 cm
B. 12 cm
C. 15 cm
D. 16 cm
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
22 tháng 7 2019
Đúng(0)
Những câu hỏi liên quan
CM
28 tháng 2 2019
Gọi độ dài hai cạnh góc vuông của tam giác lần lượt là a và b. Gọi c là độ dài cạnh huyền (a, b, c > 0)
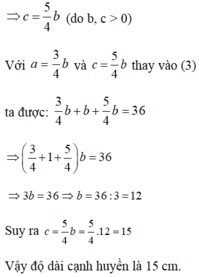
Đáp án B
6 tháng 1 2022
Gọi hai cạnh góc vuông là a, b; cạnh huyền là c;
Dựa vào tính chất Pi-ta-go, tỉ số của cạnh huyền là: \(\sqrt{3^2}+4^2=\sqrt{9}+16=5\);
Dựa vào tính chất dãy tỉ số bằng nhau, ta có:
\(\frac{a}{3}=\frac{b}{4}=\frac{c}{5}=\frac{a+b+c}{3+4+5}=\frac{36}{12}=3;\)
Vì a/3 = 3 => a = 3*3 = 9;
b/4 = 3 => b = 4*3 = 12;
c/5 = 3 => c = 5*3 = 15;
HQ
Hà Quang Minh
Giáo viên
26 tháng 9 2023
Đặt cạnh huyền của tam giác là x (\(x > 8\))
Theo giải thiết ta tính được cạnh góc vuông là \(x - 8\)
Áp dụng định lý Pitago ta tính được cạnh góc vuông còn lại là \(\sqrt {{x^2} - {{\left( {x - 8} \right)}^2}} = \sqrt {16x - 64} \)
Ta có chu vi của tam giác là \(x + \left( {x - 8} \right) + \sqrt {16x - 64} = 30\)
\(\begin{array}{l} \Leftrightarrow \sqrt {16x - 64} = 38 - 2x\\ \Rightarrow 16x - 64 = {\left( {38 - 2x} \right)^2}\\ \Rightarrow 16x - 64 = 1444 - 152x + 4{x^2}\\ \Rightarrow 4{x^2} - 168x + 1508 = 0\end{array}\)
\( \Rightarrow x = 13\) và \(x = 29\)
Thay \(x = 13\) và \(x = 29\) vào phương trình \(\sqrt {16x - 64} = 38 - 2x\) ta thấy chỉ có \(x = 13\) thảo mãn phương trình
Vậy cạnh huyền có độ dài là 13 cm.
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
15 tháng 10 2023
Câu đầu:
\(Chu.vi.HV=Chu.vi.hình.tam.giác=\dfrac{7}{12}\left(cm\right)\\ Cạnh.hình.tam.giác:\dfrac{7}{12}:3=\dfrac{7}{36}\left(cm\right)\)
Câu dưới:
Tổng thể tích nước siro dâu và nước lọc:
\(\dfrac{1}{2}+\dfrac{7}{4}=\dfrac{9}{4}\left(lít\right)\)
Số lượng cốc nước dâu rót được là:
\(\dfrac{9}{4}:\dfrac{1}{8}=18\left(cốc\right)\\ Đáp.số:18.cốc\)
Chọn A
NP
0
31 tháng 8 2023
4:
a: Gọi độ dài cạnh góc vuông cần tìm là x
Theo đề, ta có: x^2+x^2=a^2
=>2x^2=a^2
=>x^2=a^2/2=2a^2/4
=>\(x=\dfrac{a\sqrt{2}}{2}\)
b:
Độ dài cạnh là;
\(h:\dfrac{\sqrt{3}}{2}=\dfrac{2h}{\sqrt{3}}\)
5:
ΔAHB vuông tại H
=>AH^2+HB^2=AB^2
=>13^2=12^2+HB^2
=>HB=5cm
BC=5+16=21cm
ΔAHC vuông tại H
=>AH^2+HC^2=AC^2
=>AC^2=16^2+12^2=400
=>AC=20(cm)