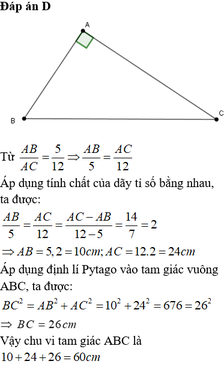
Cho △ A B C vuông tại A có A B A C = 5 12 và AC-AB=14cm. Tính chu vi của △ A B C
A. 70 cm
B. 30cm
C. 50cm
D. 60cm
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: \(AC=\sqrt{12^2+14^2}=2\sqrt{85}\left(cm\right)\)
\(BH=\dfrac{BA\cdot BC}{AC}=\dfrac{12\cdot14}{2\sqrt{85}}=\dfrac{84\sqrt{85}}{85}\left(cm\right)\)
b: Xét ΔABC có BD là đường phân giác
nên AD/AB=CD/BC
=>AD/12=CD/14
=>AD/6=CD/7
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{AD}{6}=\dfrac{CD}{7}=\dfrac{AD+CD}{6+7}=\dfrac{2\sqrt{85}}{13}\)
Do đó: \(AD=\dfrac{12\sqrt{85}}{13}\left(cm\right);CD=\dfrac{14\sqrt{85}}{13}\left(cm\right)\)

a: BC=căn 6^2+8^2=10cm
Xét ΔABC vuông tại A có sin C=AB/BC=3/5
nên góc C=37 độ
=>góc B=53 độ
b: Xét ΔABC có AD là phân giác
nên DB/AB=DC/AC
=>DB/3=DC/4=(DB+DC)/(3+4)=10/7
=>DB=30/7cm; DC=40/7cm
c: Xét tứ giác AEDF có
góc AED=góc AFD=góc FAE=90 độ
AD là phân giác của góc EAF
=>AEDF là hình vuông

a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=9^2+12^2=225\)
hay BC=15
Xét ΔABC vuông tại A có
\(\sin\widehat{B}=\dfrac{AC}{BC}=\dfrac{12}{15}=\dfrac{4}{5}\)
nên \(\widehat{B}\simeq53^0\)
Ta có: ΔABC vuông tại A(gt)
nên \(\widehat{B}+\widehat{C}=90^0\)(Hai góc nhọn phụ nhau)
hay \(\widehat{C}=37^0\)
b) Xét ΔABC có AD là đường phân giác ứng với cạnh BC(gt)
nên \(\dfrac{BD}{AB}=\dfrac{CD}{AC}\)(Tính chất tia phân giác của tam giác)
hay \(\dfrac{BD}{9}=\dfrac{CD}{12}\)
mà BD+CD=BC(D nằm giữa B và C)
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{BD}{9}=\dfrac{CD}{12}=\dfrac{BD+CD}{9+12}=\dfrac{15}{21}=\dfrac{5}{7}\)
Do đó:
\(\left\{{}\begin{matrix}BD=\dfrac{45}{7}\left(cm\right)\\CD=\dfrac{60}{7}\left(cm\right)\end{matrix}\right.\)
c) Xét tứ giác AFDE có
\(\widehat{AFD}=90^0\)
\(\widehat{AED}=90^0\)
\(\widehat{FAE}=90^0\)
Do đó: AFDE là hình chữ nhật(Dấu hiệu nhận biết hình chữ nhật)
Hình chữ nhật AFDE có AD là tia phân giác của \(\widehat{FAE}\)(gt)
nên AFDE là hình vuông(Dấu hiệu nhận biết hình vuông)

Sửa đề: cắt AB tại D.
a) Sửa đề: ΔACD=ΔECD
Xét ΔACD vuông tại A và ΔECD vuông tại E có
CD chung
\(\widehat{ACD}=\widehat{ECD}\)(CD là tia phân giác của \(\widehat{ACE}\))
Do đó: ΔACD=ΔECD(Cạnh huyền-góc nhọn)
b) Ta có: ΔACD=ΔECD(cmt)
nên DA=DE(Hai cạnh tương ứng)
Xét ΔDAE có DA=DE(cmt)
nên ΔDAE cân tại D(Định nghĩa tam giác cân)

a)Áp dụng HTL2 vào tam giác ABC cuông tại A, đường cao AH ta có:
AH2=BH.HC=9.16=144
<=>AH=√144=12((cm)
Áp dụng định lý Pytago vào tam giác vuông BHA ta có:
BA2=AH2+BH2=122+92=225
<=>BA=√225=15(cm)
Áp dụng định lý Pytago vào tam giác vuông CHA ta có:
CA2=AH2+CH2=122+162=20(cm)
Vậy AB=15cm,AC=20cm,AH=12cm

XÉT tam giác ABC vuông tại A : BC2=AB2+AC2=36+64+100
=>BC=10.
b) áp dụng tích chất đường pg trong tam giác vào tam giác abc ta có :
AB/AC=BD/DC <=> 6/8=BD/DC<=>BD/6=DC/8=K .
=> 6K=DC ; 8K=BD .
CÓ BD+DC =BC=10
<=>6K+8K=10
<=>14K=10
<=>K=5/7 .
=>DB=5/7 . 8 = 40/7 ;DC=5/7 . 6 =30/7 .
C) TG AEDF LÀ HCN VÌ : GÓC DÈ = GÓC EAF = GÓC AFD=90'.
CHU VI VÀ DIỆN TÍCH THÌ TÍNH CẠNH EA VÀ ED THÌ RA.

a) Áp dụng đinh lý Pytago ta có:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow\)\(BC^2=6^2+8^2=100\)
\(\Leftrightarrow\)\(BC=10\)
Để tính góc B bn tính tỉ số lượng giác của 1 trong 2 góc sau đó tra bảng là ra đc số đo góc đó và tính đc góc còn lại
(do mk k biết dùng bảng lượng giác nên k giúp đc phần này)
b) \(AD\)là phân giác \(\widehat{BAC}\)
\(\Rightarrow\)\(\frac{BD}{AB}=\frac{DC}{AC}\)hay \(\frac{BD}{6}=\frac{DC}{8}=\frac{BD+DC}{6+8}=\frac{10}{14}=\frac{5}{7}\)
suy ra: \(\frac{BD}{6}=\frac{5}{7}\)\(\Rightarrow\)\(BD=\frac{30}{7}\)
\(\frac{DC}{8}=\frac{5}{7}\)\(\Rightarrow\)\(DC=\frac{40}{7}\)
c) Tứ giác AEDF có: \(\widehat{A}=\widehat{F}=\widehat{E}=90^0\)
\(\Rightarrow\)Tứ giác \(AEDF\)là hình chữ nhật