Thực hiện các phép tính:
a) 3 - 5 14 + 3 20
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
17 tháng 9 2017
Đúng(0)
Những câu hỏi liên quan
S
2 tháng 6 2021
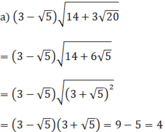
\(\dfrac{3}{5}+\dfrac{13}{25}-\dfrac{5}{9}-\dfrac{3}{7}\)
\(=\dfrac{15}{25}+\dfrac{13}{25}-\dfrac{35}{63}-\dfrac{27}{63}\)
\(=\dfrac{28}{25}-\dfrac{62}{63}=\dfrac{214}{1575}\)
29 tháng 10 2021
b: \(=15\left(141+19\right)=15\cdot160=24000\)
c: \(=2^3\cdot\left(17-14\right)=8\cdot3=24\)
NT
0
NT
1
HT
2
29 tháng 5 2022
a: \(=4\cdot2\sqrt{6}-3\cdot3\sqrt{6}+5\sqrt{6}-5\sqrt{6}\)
\(=8\sqrt{6}-9\sqrt{6}=-\sqrt{6}\)
b: \(=2\left(3-2\sqrt{2}\right)-2\left(3+2\sqrt{2}\right)\)
\(=6-4\sqrt{2}-6-4\sqrt{2}=-8\sqrt{2}\)
c: \(=\sqrt{3-\sqrt{5}}-\sqrt{3+\sqrt{5}}\)
\(=\dfrac{\sqrt{6-2\sqrt{5}}-\sqrt{6+2\sqrt{5}}}{\sqrt{2}}\)
\(=\dfrac{\sqrt{5}-1-\sqrt{5}-1}{\sqrt{2}}=-\dfrac{2}{\sqrt{2}}=-\sqrt{2}\)
R
19 tháng 11 2021
Bài 1:
a)-54
b)-8
Bài 2:
a)(x-14):5=415:413
⇔(x-14):5=42
⇔(x-14):5=16
⇔x-14=80
⇔x=94
b)7x-15x=15-175
⇔-8x=-160
⇔x=20
T
5 tháng 12 2023
a) $371+731-271-531$
$=(371-271)+(731-531)$
$=100+200$
$=300$
b) $57+58+59+60+61-17-18-19-20-21$
$=(57-17)+(58-18)+(59-19)+(60-20)+(61-21)$
$=40+40+40+40+40$
$=40\cdot5$
$=200$
c) $9-10+11-12+13-14+15-16$
$=(9-10)+(11-12)+(13-14)+(15-16)$
$=-1+(-1)+(-1)+(-1)$
$=-1\cdot4$
$=-4$
$\text{#}Toru$
6 tháng 6 2021
Bài 2:
a)\(\dfrac{1}{3}\sqrt{x-2}-\dfrac{2}{3}\sqrt{9x-18}+6\sqrt{\dfrac{x-2}{81}}=-4\) (đk: \(x\ge2\))
\(\Leftrightarrow\dfrac{1}{3}\sqrt{x-2}-\dfrac{2}{3}\sqrt{9\left(x-2\right)}+\dfrac{6}{\sqrt{81}}\sqrt{x-2}=-4\)
\(\Leftrightarrow\dfrac{1}{3}\sqrt{x-2}-2\sqrt{x-2}+\dfrac{2}{3}\sqrt{x-2}=-4\)
\(\Leftrightarrow-\sqrt{x-2}=-4\) \(\Leftrightarrow x-2=16\)
\(\Leftrightarrow x=18\) (thỏa)
Vậy...
b)\(\sqrt{9x^2+12x+4}=4x\)(Đk:\(9x^2+12x+4\ge0\))
\(\Leftrightarrow\left\{{}\begin{matrix}4x\ge0\\9x^2+12x+4=16x^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\-7x^2+12x+4=0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\-7x^2+14x-2x+4=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\\left(x-2\right)\left(-7x-2\right)=0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\\left[{}\begin{matrix}x=2\\x=-\dfrac{2}{7}\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow x=2\) (tm đk)
Vậy...
c) \(\sqrt{x-2\sqrt{x-1}}=\sqrt{x-1}\) (đk: \(x\ge1\))
\(\Leftrightarrow x-2\sqrt{x-1}=x-1\)
\(\Leftrightarrow\sqrt{x-1}=\dfrac{1}{2}\) \(\Leftrightarrow x=\dfrac{5}{4}\) (tm)
Vậy...
