Phần tự luận
Nội dung câu hỏi 1
Cho đường tròn (O, 15 cm) và đường tròn (O', 20 cm) cắt nhau tại M và N. Biết MN = 24 cm. O và O' nằm khác phía so với MN
a) Chứng minh OO' vuông góc với MN
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
24 tháng 6 2017
c) Xét tam giác OMO' có:
O M 2 + O ' M = 15 2 + 20 2 = 625 = 25 2 = O O '
= 152 + 202 = 625 = 252 = OO'2
⇒ Tam giác OMO' vuông tại M
HH
15 tháng 7 2020
Bài này hơi khó , bạn tự vẽ hình với làm câu a) nhé 😅😅
b)
00' cắt AB tại H
\(\Rightarrow AH=\frac{AB}{2}=\frac{24}{2}=12\)
Áp đụng Pythagore cho tam giác vuông AOH
\(OH=\sqrt{\left(20^2-12^2\right)}=16\)
Pythagore ▲vuông O'AH Áp dụng Pythagore cho tam giác vuông O'AH
\(O'H=\sqrt{\left(15^2-12^2\right)}=9\)
\(\Rightarrow OO'=OH+O'H=16+9=25cm\)
Vậy : OO' dài 25cm
CM
30 tháng 6 2019
- Trường hợp 1: O và O' nằm khác phía đối với AB
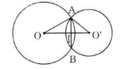
Gọi I là giao điểm của OO' và AB. Theo tính chất đường nối tâm ta có:
AB ⊥ OO' và AI = IB = 12
Áp dụng định lí Pitago, ta được:
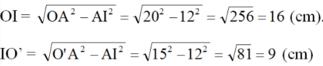
Vậy OO' = OI + IO' = 16 + 9 = 25 (cm)
- Trường hợp 2: O và O' nằm cùng phía đối với AB
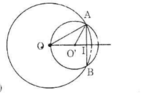
Tương tự như trường hợp 1, ta có:
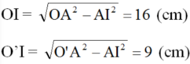
Vậy OO' = OI – O'I = 16 – 9 = 7 (cm).
CM
23 tháng 8 2019
- Trường hợp 1: O và O' nằm khác phía đối với AB
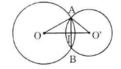
Gọi I là giao điểm của OO' và AB. Theo tính chất đường nối tâm ta có:
AB ⊥ OO' và AI = IB = 12
Áp dụng định lí Pitago, ta được:
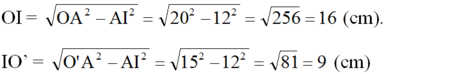
Vậy OO' = OI + IO' = 16 + 9 = 25 (cm)
- Trường hợp 2: O và O' nằm cùng phía đối với AB
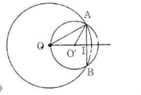
Tương tự như trường hợp 1, ta có:
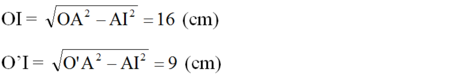
Vậy OO' = OI – O'I = 16 – 9 = 7 (cm).
a) Xét đường tròn (O; 15 cm) có: OM = ON = 15 cm
⇒ O nằm trên đường trung trực của MN
Xét đường tròn (O'; 20 cm) có: O'M = O'N = 20 cm
⇒ O' nằm trên đường trung trực của MN
⇒ OO' là đường trung trực của MN hay OO' ⊥ MN