Từ một điểm M nằm ngoài đường tròn (O) vẽ hai tiếp tuyến MA, MB với đường tròn (A, B là các tiếp điểm). Vẽ AH ⊥ MB, BK ⊥ MA (H∈MB,K∈MA). Gọi C là giao điểm của AH và BK. Chứng minh rằng:
b) Ba điểm M, O, C thẳng hàng
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

CM
29 tháng 11 2017
a) Ta có:
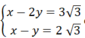
Xét tứ giác AOBC có:
AO // BC
AC // BO
⇒ Tứ giác AOBC là hình bình hành
Mà OA = OC = R
⇒ Tứ giác AOBC là hình thoi

CM
18 tháng 5 2019
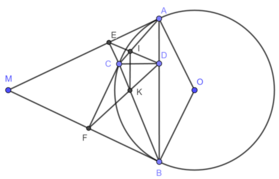

( góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn cung BC)


CM
13 tháng 8 2019
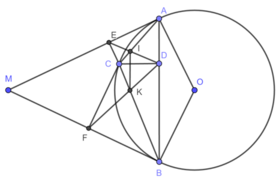

(góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn cung AC) (2)

(góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn cung CB) (5)

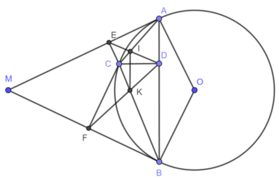

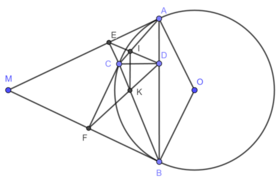

b) Do AOBC là hình thoi nên AB ⊥ CO
Lại có MA và MB là 2 tiếp tuyến cắt nhau của (O) nên AB ⊥ MO
⇒ M,C,O thẳng hàng.