Cho đường tròn (O), đường kính AB, điểm C nằm giữa A và O. Vẽ đường tròn (O') có đường kính CB
c) Gọi K là giao điểm của DB và đường tròn (O'). Chứng minh rằng 3 điểm E, C, K thẳng hàng.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
20 tháng 9 2017
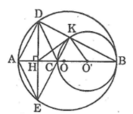
Tam giác ABD nội tiếp trong đường tròn (O) có Ab là đường kính nên vuông tại D
Suy ra: AD ⊥ BD
Tứ giác ADCE là hình thoi nên EC // AD
Suy ra: EC ⊥ BD (1)
Tam giác BCK nội tiếp trong đường tròn (O’) có BC là đường kính nên vuông tại K
Suy ra: CK ⊥ BD (2)
Từ (1) và (2) suy ra EC trùng với CK
Vậy E, C, K thẳng hàng.
CM
20 tháng 10 2018
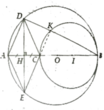
a, (O) và (I) tiếp xúc trong với nhau
b, Tứ giác ADCE là hình thoi
c, Có CK ⊥ AB, AD ⊥ DB
=> CK//AD mà CE//AD
=> B,K,D thẳng hàng
d, H K D ^ = H D K ^ ; I K B ^ = I B K ^
=> H K D ^ + I K B ^ = I B K ^ + H D K ^ = 90 0
=> I K H ^ = 90 0
HH
20 tháng 1 2021
a) Ta có : OB - O'B = OO'
=> đường tròn (O) và (O'O tiếp xúc trong
b) Ta có : \(OA\perp DE\left(gt\right)\)
=> HD = HE hay H là trung điểm của DE
Theo (gt) : HA = HC
T/g ADCE có 2 đường chéo vuông góc với nhau tại trung điểm mỗi đường
=> T/g ADCE là hình thoi
c) Xét tam giác KBC có :
O'K = O'B = O'C (=bk)
\(\Rightarrow O'K=\frac{1}{2}BC\)
=> Tam giác KBC vuông tại K => \(CK\perp DB\left(1\right)\)
Xét tam giác ADB có :
OD = OA = OB ( =bk )
\(\Rightarrow OD=\frac{1}{2}AB\)
=> Tam giác ADB vuông tại D \(\Rightarrow AD\perp DB\left(2\right)\)
Từ (1) và (2) => CK // AD (*)
Theo ( c/m câu a ) : Tứ giác ADCE là hình thoi
=> CE // AD ( ** )
Từ (*) và (**) => CE và CK là 2 đường thẳng trùng nhau
Vậy : 3 điểm E , C , K thẳng hàng ( đpcm )
NM
Nguyễn Minh Quang
Giáo viên
20 tháng 1 2021
a. hai đường tròn tiếp xúc trong
b.ADCE là tứ giác thoi do có hai đường chéo vuông góc vcowis nhau tại trung điểm của mỗi đường
c. ta dễ thấy AD//CẺ mà AE vuông gó c với BD nên CE vuông BD
mà CK cũng vuông góc với BD nến C,K,E thẳng hàng
d. ta có do tam giác EKD vuông nên \(HK^2=HD^2=HA.HB=HC.HB\)
do \(HK^2=HC.HB\) nên HK là tiếp tuyến của O'
1 tháng 10 2021
a: Xét (O) có
OH là một phần đường kính
DE là dây
OH\(\perp\)DE tại H
Do đó: H là trung điểm của DE
Xét tứ giác CDAE có
H là trung điểm của đường chéo DE
H là trung điểm của đường chéo CA
Do đó: CDAE là hình bình hành
mà CA\(\perp\)DE
nên CDAE là hình thoi
18 tháng 3 2020
Khá khó nên gạch xóa hơi nhiều
Link ảnh: https://imgur.com/a/cE1k5pV
c) Ta có:
∠(CKB) = 90 0 (Góc nội tiếp chắn nửa đường tròn (O')) ⇒ CK ⊥ BD
∠(ADB) = 90 0 (Góc nội tiếp chắn nửa đường tròn (O)) ⇒ AD ⊥ BD
⇒ CK // AD
Lại có: CE // AD (Tứ giác ADCE là hình thoi)
⇒ C, E, K thẳng hàng