Cho hình chóp tứ giác đều có cạnh đáy bằng a và biết diện tích xung quanh gấp đôi diện tích đáy. Thể tích của khối chóp đã cho bằng
A. a 3 3 2
B. a 3 3 3
C. a 3 3 6
D. a 3 3 12
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D.
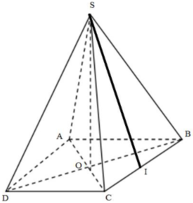
Phương pháp:
+) Gọi b là độ dài cạnh bên, sử dụng giả thiết diện tích xung quanh gấp đôi diện tích đáy biểu diễn b theo a.
+) Gọi O = AC ∩ BD ⇒ SO ⊥ (ABCD)
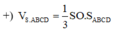
Cách giải:
Gọi b là độ dài cạnh bên, I là trung điểm của BC ⇒ SI ⊥ BC
Tam giác SIB vuông tại I
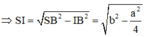
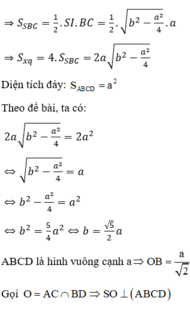
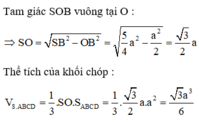

Đáp án là D
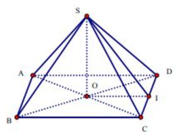
Thể tích khối chóp
Gọi O là tâm của hình vuông, I là trung điểm DC thì SI ⊥ CD .
Đặt SO = h. Có
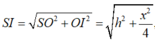
![]()
Suy ra:
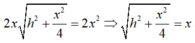
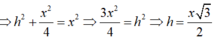
Lúc đó:
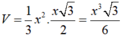

Đáp án A
Gọi O là tâm của hình vuông ABCD.
Do S.ABCD là hình chóp đều nên SO ⊥ (ACBD)
Suy ra, OB là hình chiếu vuông góc của SB lên mp(ABCD)

Gọi chiều cao của hình chớp là h. Khi đó ta tính được diện tích xung quanh của hình chóp là
Theo yêu cầu bài toán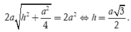
Thể tích khối chóp là: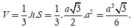
Chọn C.