Cho tứ giác ABCD, trong đó A ^ + B ^ = 140 0 . Tổng C ^ + D ^ = ?
A. 220 0
B. 120 0
C. 60 0
D. 100 0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Cho tứ giác ABCD, trong đó A ^ + B ^ = 140 0 . Tổng C ^ + D ^ = ?
A. 220 0
B. 120 0
C. 60 0
D. 100 0



Đáp án cần chọn là: A
Trong tứ giác ABCD có: C ^ + D ^ = 360 ° - A ^ + B ^ = 360 ° - 140 ° = 220 °

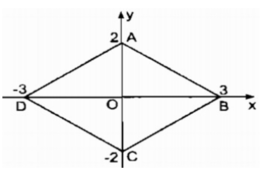
Ta có: A(0;2) và C(0;-2) là hai điểm đối xứng qua O(0;0)
⇒ OA = OC
B(3;0) và D(-3; 0) là hai điểm đối xứng qua O(0;0)
⇒ OB = OD
Tứ giác ABCD là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm của mỗi đường)
Lại có: Ox ⊥ Oy hay AC ⊥ BD.
Vậy tứ giác ABCD là hình thoi
Trong ∆ OAB vuông tại O, theo định lý Pi-ta-go ta có:
A B 2 = O A 2 + O B 2
A B 2 = 2 2 + 3 2 = 4 + 9 = 13
AB = 13
Vậy chu vi của hình thoi bằng 4 13

Trong chương trình lớp 8 chỉ xét tứ giác lồi, có tổng số đo 4 góc = 360 độ.
Giả thiết bạn đưa ra tứ giác ABCD có : A + B + C + D = 380 độ là ko chính xác nhé.
bạn viết chính xác lại đề đi nhé

Bài 1)
Trên AD lấy E sao cho AE = AB
Xét ∆ACE và ∆ACB ta có :
AC chung
DAC = BAC ( AC là phân giác)
AB = AE (gt)
=> ∆ACE = ∆ACB (c.g.c)
=> CE = CB (1)
=> AEC = ABC = 110°
Mà AEC là góc ngoài trong ∆EDC
=> AEC = EDC + ECD ( Góc ngoài ∆ bằng tổng 2 góc trong không kề với nó)
=> ECD = 110 - 70
=> EDC = 40°
Xét ∆ EDC :
DEC + EDC + ECD = 180 °
=> CED = 180 - 70 - 40
=> CED = 70°
=> CED = EDC = 70°
=> ∆EDC cân tại C
=> CE = CD (2)
Từ (1) và (2) :
=> CB = CD (dpcm)
b) Ta có thể thay sao cho tổng 2 góc đối trong hình thang phải = 180°