Cho tam giác ABC có BC = 16cm ,đường cao AH = 8cm. Gọi M và N lần lượt là trung điểm của AB và AC. Tính diện tích của tứ giác MNCB?
A. 48 c m 2
B. 40 c m 2
C. 54 c m 2
D. 60 c m 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔABC có
P là trung điểm của AC
N là trung điểm của BC
Do đó: PN là đường trung bình của ΔBAC
Suy ra: PN//AB và \(PN=\dfrac{AB}{2}\)
mà M\(\in\)AB và \(AM=\dfrac{AB}{2}\)
nên PN//AM và PN=AM
Xét tứ giác AMNP có
PN//AM
PN=AM
Do đó: AMNP là hình bình hành
mà \(\widehat{PAM}=90^0\)
nên AMNP là hình chữ nhật

a: Xét ΔCAB có CP/CA=CN/CB
nên PN//AB và PN=AB/2
=>PN//AM và PN=AM
=>AMNP là hình bình hành
mà góc PAM=90 độ
nên AMNP là hình chữ nhật
b: \(AC=\sqrt{10^2-8^2}=6\left(cm\right)\)
AH=6*8/10=4,8cm

Xét tam giác ABC có M và N lần lượt là trung điểm của AB và AC nên MN là đường trung bình của tam giác ABC
Suy ra: MN// BC và
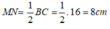
Tương tự, có NP là đường trung bình của tam giác nên: NP // AB
Xét tứ giác MNPB có MN// BC và NP // AB
Suy ra: tứ giác MNPB là bình hành.
Tam giác ABC có đường cao AH = 10cm nên đường cao ứng với cạnh đáy của hình bình hành MNPB là:
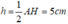
Diện tích hình bình hành MNPB là:
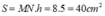
Chọn đáp án C

a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay \(BC=\sqrt{100}=10cm\)
Xét ΔABC có AH là đường cao ứng với cạnh BC nên
\(S_{ABC}=\dfrac{AH\cdot BC}{2}\)(1)
Ta có: ΔABC vuông tại A(gt)
nên \(S_{ABC}=\dfrac{AB\cdot AC}{2}\)(2)
Từ (1) và (2) suy ra \(AH\cdot BC=AB\cdot AC\)
\(\Leftrightarrow AH\cdot10=6\cdot8=48\)
hay \(AH=\dfrac{48}{10}=4.8cm\)
Vậy: AH=4,8cm
b) Xét tứ giác AEHF có
\(\widehat{EAF}=90^0\)(ΔABC vuông tại A, E∈AB, F∈AC)
\(\widehat{AEH}=90^0\)(HE⊥AB)
\(\widehat{AFH}=90^0\)(HF⊥AC)
Do đó: AEHF là hình chữ nhật(Dấu hiệu nhận biết hình chữ nhật)
⇒AH=EF(Hai đường chéo của hình chữ nhật AEHF)
mà AH=4,8cm(cmt)
nên EF=4,8cm
Vậy: EF=4,8cm

a) Xét ΔABC vuông tại A và ΔHBA vuông tại H có
\(\widehat{ABC}\) chung
Do đó: ΔABC∼ΔHBA(g-g)

a, Xét tam giác ABC vuông tại A, đường cao AH
\(AB^2+AC^2=BC^2\Rightarrow BC^2=64+225=289\Rightarrow BC=17\)cm
Xét tam giác AHC và tam giác BAC ta có :
^AHC = ^BAC = 900
^C _ chung
Vậy tam giác AHC ~ tam giác BAC ( g.g )
\(\Rightarrow\frac{AH}{AB}=\frac{AC}{BC}\)( tỉ số đồng dạng )
\(\Rightarrow AH.BC=AB.AC\Rightarrow AH=\frac{AB.AC}{BC}=\frac{8.15}{17}=\frac{120}{17}\)cm
b, Vì MH vuông AB
NA vuông AB
=> MH // NA tương tự ta có : MH // AN
=> tứ giác AMNH là hình bình hành
mà ^HNA = 900 ; ^BAC = 900 ; ^HMA = 900
=> tứ giác AMHN là hình vuông

a) Xét ΔABC có
F là trung điểm của AC(gt)
M là trung điểm của BC(gt)
Do đó: FM là đường trung bình của ΔABC(Định nghĩa đường trung bình của tam giác)
⇒FM//AB và \(FM=\dfrac{AB}{2}\)(Định lí 2 về đường trung bình của tam giác)
mà E∈AB và \(AE=\dfrac{AB}{2}\)(E là trung điểm của AB)
nên FM//AE và FM=AE
Xét tứ giác AEMF có
FM//AE(cmt)
FM=AE(cmt)
Do đó: AEMF là hình bình hành(Dấu hiệu nhận biết hình bình hành)
Hình bình hành AEMF có \(\widehat{FAE}=90^0\)(ΔABC vuông tại A)
nên AEMF là hình chữ nhật(Dấu hiệu nhận biết hình chữ nhật)

a) Xét ΔABC có
M là trung điểm của AB(gt)
N là trung điểm của AC(gt)
Do đó: MN là đường trung bình của ΔABC(Định nghĩa đường trung bình của tam giác)
Suy ra:MN//BC và \(MN=\dfrac{BC}{2}\)(Định lí 2 về đường trung bình của tam giác)
hay \(BC=2\cdot MN=2\cdot8=16\left(cm\right)\)
b) Xét tứ giác BMNC có MN//BC(cmt)
nên BMNC là hình thang(Định nghĩa hình thang)
Hình thang BMNC có \(\widehat{B}=\widehat{C}\)(ΔABC cân tại A)
nên BMNC là hình thang cân
Xét tam giác ABC có M và N lần lượt là trung điểm của AB và AC nên MN là đường trung bình của tam giác ABC.
Suy ra: MN // BC và
Do đó, tứ giác MNCB là hình thang .
Vì AH = 8cm nên đường cao kẻ từ M đến BC bằng
Diện tích hình thang MNCB là :
Chọn đáp án A