Cho hình vuông ABCD có tâm I. Trên tia BC lấy điểm E sao cho BE = AI.
a) Xác định một phép dời hình biến A thành B và I thành E
b) Dựng ảnh của hình vuông ABCD qua phép dời hình ấy.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
4 tháng 5 2018
Đáp án D
Phát biểuđúng: a , c, e, f, g, i, j, l
b. Phép biến hình biến đường tròn thành đường tròn có bán kính bằng nó có thể là phép tịnh tiến
d. Phép tịnh tiến biến đường tròn thành đường tròn có cùng bán kính
h. Với bất kì 2 điểm A, B và ảnh A’, B’ của chúng qua 1 phép dời hình, ta luôn có AB = A’B’.
k. Nếu phép dời hình biến điểm A thành điểm B thì nó cũng biến điểm B thành A (phát biểu không đúng với phép tịnh tiến)
CM
7 tháng 12 2017
Đ E I ( 1 ) = ( 8 ) ; T D I → ( 8 ) = ( 3 ) .
A. Phép đối xứng tâm I và phép đối xứng trục IB thì (1) không biến thành hình nào từ (2) đến (8).
B. Phép đối xứng tâm I và phép quay tâm I góc quay 90 o (1) không biến thành hình nào từ (2) đến (8)
D.phép tịnh tiến theo A I → và phép đối xứng tâm I thì hình (1) thành hình (2)
Đáp án C
CM
12 tháng 4 2019
- Ảnh của A, B, O qua phép quay tâm O góc 90o lần lượt là: D, A, O
- Ảnh của D, A, O qua phép đối xứng qua đường thẳng BD là: D, C, O
CM
2 tháng 7 2019
Đáp án A
Nhữngphát biểu sai: d; f; i
d) Qua phép đối xứng trục, đoạn thẳng AB biến thành đoạn thẳng song song và bằng nó hoặc là chính nó.
f) Qua phép đối xứng trục Đa, tam giác có một đỉnh nằm trên a sẽ biến thành chính nó ( chỉ trong trường hợp tam giác đều hoặc tam giác cân cóđỉnh nằm trên trục đối xứng)
i) Hình chữ nhật có 2 trục đối xứng
CM
27 tháng 11 2019
- Phép đối xứng qua tâm I biến ΔAEI thành ΔCFI
- Phép đối xứng qua trục d biến ΔCFI thành ΔFCH
CM
15 tháng 1 2017
Đáp án A.
Ta có hình vẽ bên.
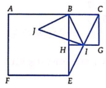
Từ A C = 3 ⇒ A B = B E = E F = F A = 2 B C = C G = G H = H B = 1 . Do I = E C ∩ G H ⇒ I là trung điểm của HG. Suy ra B I = B H 2 + H G 2 2 = 1 2 + 1 2 2 = 5 2
Q B ; - 90 ° ( I ) = J ⇒ B I ⊥ B J B I = B J ⇒ ∆ B I J vuông cân tại B.
Vậy I J = B I 2 = 5 2 . 2 = 10 2
Gọi F là phép đối xứng qua đường trung trực d của cạnh AB, G là phép đối xứng qua đường trung trực d' của cạnh IE. Khi đó F biến AI thành BI, G biến BI thành BE. Từ đó suy ra phép dời hình có được bằng cách thực hiện liên tiếp hai phép biến hình F và G sẽ biến AI thành BE.
Hơn nữa gọi J là giao của d và d', thì dễ thấy JA = JB, JI = JE và 2(JI, JB) = (JI, JE) = 45 ο
(vì JE / /IB). Do đó theo kết quả của bài 1.21, phép dời hình nói trên chính là phép quay tâm J góc 45 ο
Lưu ý. Có thể tìm được nhiều phép dời hình biến AI thành BE.
b) F biến các điểm A, B, C, D thành B, A, D, C; G biến các điểm B, A, D, C thành B, A', D', C'. Do đó ảnh của hình vuông ABCD qua phép dời hình nói trên là hình vuông BA'D'C' đối xứng với hình vuông BADC qua d'