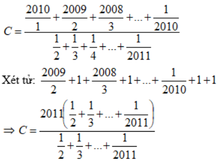
T í n h : C = 2010 1 + 2009 2 + 2008 3 + . . . + 1 2010 1 2 + 1 3 + 1 4 + . . . + 1 2011
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
24 tháng 1 2019
Đúng(0)
Những câu hỏi liên quan
19 tháng 2 2022
\(\Leftrightarrow\dfrac{x+1}{2010}+1+\dfrac{x+2}{2009}+1+...+\dfrac{x+2009}{2}+1+\dfrac{x+2010}{1}+1=0\)
=>x+2011=0
hay x=-2011
NT
0
3 tháng 3 2015
\(C=\frac{\frac{1}{2008}-\frac{1}{2009}-\frac{1}{2010}}{\frac{5}{2008}-\frac{5}{2009}-\frac{5}{2010}}+\frac{\frac{2}{2007}-\frac{2}{2008}-\frac{2}{2009}}{\frac{3}{2007}-\frac{3}{2008}-\frac{3}{2009}}\)
\(=\frac{\frac{1}{2008}-\frac{1}{2009}-\frac{1}{2010}}{5.\left(\frac{1}{2008}-\frac{1}{2009}-\frac{1}{2010}\right)}+\frac{2.\left(\frac{1}{2007}-\frac{1}{2008}-\frac{1}{2009}\right)}{3.\left(\frac{1}{2007}-\frac{1}{2008}-\frac{1}{2009}\right)}\)
\(=\frac{1}{5}+\frac{2}{3}\)
\(=\frac{13}{15}\)
R
0
TK
1
LM
17 tháng 3 2018
Ta có: \(H=2^{2010}-2^{2009}-2^{2008}-...-2-1\)
\(=2^{2010}-\left(2^{2009}+2^{2008}+...+2+1\right)\)
Đặt \(A=2^{2009}+2^{2008}+...+2+1\)
\(\Rightarrow2A=2^{20010}+2^{2009}+...+2^2+2\)
\(\Rightarrow2A-A=\left(2^{20010}+2^{2009}+...+2^2+2\right)-\left(2^{2009}+2^{2008}+...+2+1\right)\)\(\Rightarrow A=\left(2^{2010}-1\right)+\left(2^{2009}-2^{2009}\right)+\left(2^{2008}-2^{2008}\right)+...+\left(2-2\right)\)\(\Rightarrow A=2001-1\)
\(\Rightarrow H=2^{2010}-\left(2^{2010}-1\right)\)
\(\Rightarrow H=2^{2010}-2^{2010}+1=1\)
Thay \(H=1\) vào biểu thức \(2010^H\)
\(\Rightarrow2010^H=2010^1=1\)
Vậy \(2010^H=1\)
NT
1
A
18 tháng 3 2017
Ta có 2H = 2.(22010 - 22009 - 22008 - ... - 2 -1)
2H = 22011 - 22010 - 22009 - ... - 22 - 2
2H - H = 22011 - 22010 - 22009 - ... - 22 - 2 - 22010 + 22009 + 22008 + ... + 2 + 1
H = 22011 - (22010 + 22010) - (22009 - 22009) - (22008 - 22008) - ... - (2 - 2) + 1
H = 1
=> 2010H = 20101 = 2010
NT
1
19 tháng 3 2017
*2010/1+2009/2+...+1/2010
=(2009/2+1)+(2008/3+1)+...+(1/2010+1)+1
=2011/2+2011/3+..+2011/2010+2011/2011
=2011(1/2+1/3+1/4+...+1/2011)
=> C=2011/1=2011