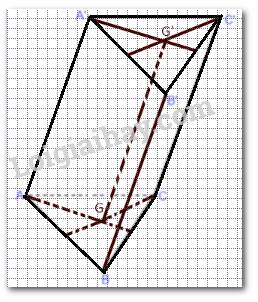
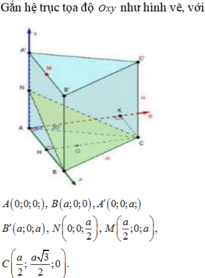
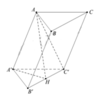
Cho lăng trụ đứng ABC. A’B’C’ có tất cả các cạnh bằng a và có G, G' lần lượt là trọng tâm của hai tam giác ABC và A’B’C’ (tham khảo hình vẽ).
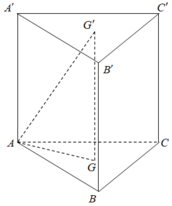
Thiết diện tạo bởi mặt phẳng (AGG') với hình lăng trụ đã cho là
A. Tam giác vuông
B. Tam giác cân
C. Hình vuông
D. Hình chữ nhật

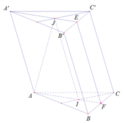
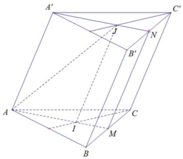
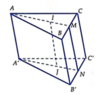



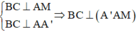
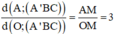
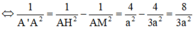
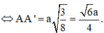
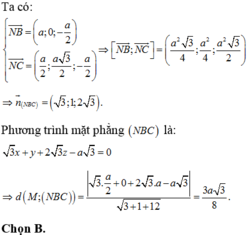
Chọn D
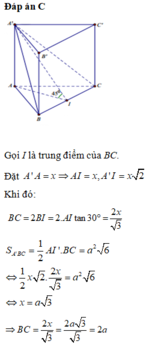
Gọi M, M' lần lượt là trung điểm của BC và B’C’. Khi đó thiết diện của lăng trụ tạo bởi mặt phẳng (AGG') là hình chữ nhật AMM'A’.
Mà A M ’ = a . s i n 60 0 = a 3 2 ≠ A A ’
Nên AMM’A’ không thể là hình vuông.