Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB=2a, BC=a. Các cạnh bên của hình chóp cùng bằng a 2 . Tính góc giữa hai đường thẳng AB và SC.
A. 45 °
B. 30 °
C. 60 °
D. arctan 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

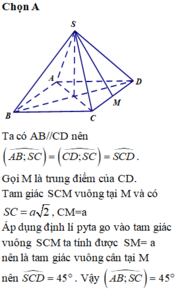

Do \(\left(SC;\left(ABCD\right)\right)=45^0;SA\perp\left(ABCD\right)\)
nên \(\left\{{}\begin{matrix}\left(SC;AC\right)=45^0\\AS\perp AC\end{matrix}\right.\)\(\Rightarrow AS=AC=\sqrt{AB^2+BC^2}=\sqrt{a^2+a^2}=a\sqrt{2}\)
\(\Rightarrow V_{S.ABCD}=\dfrac{1}{6}.\left(AD+BC\right).AB.AS\)
\(=\dfrac{1}{6}\left(2a+a\right).a.a\sqrt{2}=\dfrac{\sqrt{2}}{2}a^3\)

Đáp án D
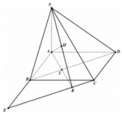
Dựng ![]()
Dựng ![]()
Khi đó Cx cắt AB tại E và AK tại I suy ra BI là đường trung bình của ∆AEK ( Do BD qua trung điểm O của AC)
Ta có: 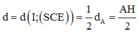
Do 
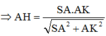
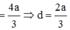

Đáp án C
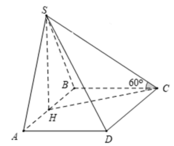
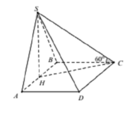
Ta có: H C = B H 2 + B C 2 = a 2
S H = H C . tan S C H = a 2 . tan 60 ∘ = a 6 A C = B A 2 + B C 2 = a 5 , S B = S H 2 + H B 2 = a 7
Ta có: S B → . A C → = S H → + H B → . A C → = H B . A C . cos B A C
⇔ S B → . A C → = H B . A C . A B A C = 2 a 2 S B . A C = a 7 . a 5 = a 2 35 ⇒ c os S B , A C = S B → . A C → S B . A C = 2 a 2 a 2 35 ⇒ S B , A C = 70 o 14 ' 28 , 22 ' '


Vì SA ⊥ (ABCD) nên AC là hình chiếu vuông góc của SC lên mặt phẳng (ABCD).
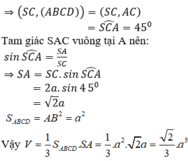

Đáp án A
Phương pháp: Sử dụng công thức ![]()
Cách giải: ![]()
Ta có ![]()
Xét tam giác vuông SHC có ![]()
Ta có:
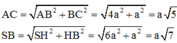
Ta có:
![]()
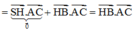
![]()
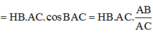
![]()
Lại có ![]()