Cho hình chóp S. ABCD có đáy là hình vuông cạnh a. S A = a 2 và SA vuông góc mặt phẳng đáy. Góc giữa cạnh bên SC với đáy bằng
A. 60⁰.
B. 30⁰.
C. 45⁰.
D. 90⁰.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

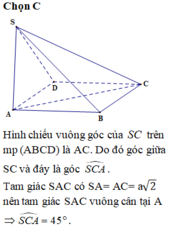

Gọi O là giao điểm của AC và BD. Dễ thấy \(\Delta OAB\) vuông tại O và \(OB=\dfrac{a\sqrt{3}}{2}\). Từ đó \(OA=\sqrt{AB^2-OB^2}=\sqrt{\left(\dfrac{\sqrt{3}}{2}a\right)^2-a^2}=\sqrt{\dfrac{1}{4}a^2}=\dfrac{a}{2}\) \(\Rightarrow AC=a\).
Vì \(SA\perp mp\left(ABCD\right)\) nên \(SA\perp AC\) tại A hay \(\Delta SAC\) vuông tại A.
Lại có \(\tan SAC=\dfrac{SA}{AC}=\dfrac{a\sqrt{3}}{a}=\sqrt{3}\) nên \(\widehat{SAC}=60^o\), suy ra góc giữa SC và mp(ABCD) bằng 60o \(\Rightarrow\) Chọn A
Chỗ \(\widehat{SAC}\) em sửa lại là \(\widehat{SCA}\) mới đúng ạ.

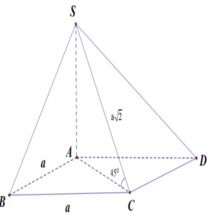
Vì SA ⊥ (ABCD) nên AC là hình chiếu vuông góc của SC lên mặt phẳng (ABCD).
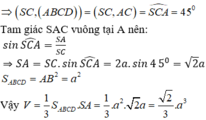


Vì SA ⊥ (ABCD) nên AC là hình chiếu vuông góc của SC lên mặt phẳng (ABCD).
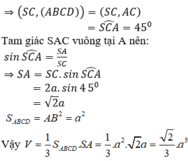

Kẻ SH vuông góc với AB. Do (SAB) vuông góc với đáy nên hình chiều của S trên (ABCD) chính là H.
Mặt khác tam giác SAB cân tại S nên H là trung điểm của AB.
\(CH=\sqrt{BH^2+BC^2}=\sqrt{\dfrac{a^2}{4}+a^2}=\dfrac{a\sqrt{5}}{2}\)
Góc giữa SC và đáy là góc SCH nên \(\widehat{SCH}=45^0\)
\(SH=CH.\tan 45^0=\dfrac{a\sqrt{5}}{2}\)
\(S_{ABCD}=a^2\)
Vậy \(V_{SABCD}=\dfrac{1}{3}.SH.S_{ABCD}=\dfrac{a^3\sqrt{5}}{6}\)
bh tính kiểu gì vậy bạn
mà bạn xác định góc giữa sc và mặt đáy phải là góc SCA chứ
giải thích hộ mình với

\(SA \bot \left( {ABCD} \right) \Rightarrow \left( {SC,\left( {ABCD} \right)} \right) = \left( {SC,AC} \right) = \widehat {SCA}\)
\(ABCD\) là hình vuông \( \Rightarrow AC = \sqrt {A{B^2} + B{C^2}} = b\sqrt 2 \)
\(\cos \widehat {SCA} = \frac{{AC}}{{SC}} = \frac{1}{2} \Rightarrow \widehat {SCA} = {60^ \circ }\)
Vậy \(\left( {SC,\left( {ABCD} \right)} \right) = {60^ \circ }\)
Chọn A.

Xác định được ![]()
Vì M là trung điểm SA nên
![]()
Kẻ ![]() và chứng minh được
và chứng minh được ![]() nên
nên ![]()
Trong
∆
vuông MAD tính được ![]()
Chọn A.