Cho hình chóp S.ABCD có đáy ABCD là hình vuông và S A ⊥ A B C D . Gọi M, N, P lần lượt là trung điểm AB, BC và SB. Mệnh đề nào sau đây là sai?
A. M N P / / S A C
B. B D ⊥ M N P
C. Góc giữa SC và BD là 60°
D. B C ⊥ M P
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Kẻ Ax//BC, H I ⊥ A x , H K ⊥ S I . Gọi M là trung điểm của AB
⇒ d ( B C , S A ) = d ( B C , ( S A x ) ) = 4 3 d ( H , S A x )
Ta có A I ⊥ ( S H I ) ⇒ A I ⊥ H K ⇒ H K ⊥ ( S A I ) ⇒ d ( H , ( S A x ) ) = H K
Góc giữa SC và (ABC) là góc S C H ^ = 60 °
Ta có H C = C M 2 + M H 2 = a 3 2 2 + a 4 2 = a 13 4
⇒ S H = H C . tan 60 ° = a 39 4
H I = A H . sin 60 ° = 3 4 . a . 3 2 = a . 3 3 8
Ta có H K 2 = H I 2 . S H 2 H I 2 + S H 2 = 351 . a 2 61 ⇒ H K = a 351 61
⇒ d ( B C , S A ) = 4 3 . d H , ( S A x ) = 4 a 351 3 61

Đáp án B
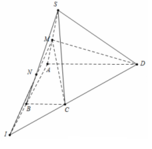
Gọi I = A B ∩ C D và N = S B ∩ M I khi đó giao điểm của SB và (MCD) là N. Dễ thấy MN và CD cắt nhau

Chọn C
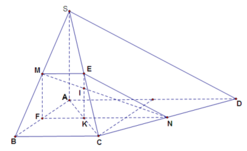
Ta gọi E, F lần lượt là trung điểm của SC, AB
Ta có ME//NF(do cùng song song với BC. Nên tứ giác MENF là hình thang, và 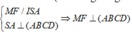
hay tứ giác MENF là hình thang vuông tại M, F
![]()
![]()
Ta có: 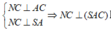 hay E là hình chiếu vuông góc của N lên (SAC)
hay E là hình chiếu vuông góc của N lên (SAC)
Từ đó ta có được, góc giữa MN và (SAC) là góc giữa MN và CI
Suy ra, gọi
α
là góc giữa MN và (SAC) thì ![]()
![]()
![]()
![]()