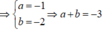Số tiếp tuyến của đổ thị hàm số y = x + 2 2 x + 3 mà cắt trục hoành, trục tung lần lượt tại A và B sao cho ∆0AB cân là:
A. 0
B. 1
C. 2
D. 4
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
27 tháng 12 2017
Đúng(0)
Những câu hỏi liên quan
CM
26 tháng 1 2017
Đáp án B.
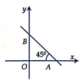
Δ O A B cân =>Tiếp tuyến tạo với Ox một góc 45 °
Hệ số góc của tiếp tuyến tại M x 0 ; y 0 ∈ ( C ) là y ' ( x 0 ) = ± tan 45 °
⇔ − 1 2 x 0 + 3 2 = 1 ( V N ) − 1 2 x 0 + 3 2 = − 1 ⇔ 2 x 0 + 3 = 1 2 x 0 + 3 = − 1 ⇔ x 0 = − 2 x 0 = − 1
-Với x 0 = − 1 ⇒ y 0 = 1 ⇒ Phương trình tiếp tuyến:
y = − 1 ( x + 1 ) + 1 ⇒ y = − x
-Với x 0 = − 2 ⇒ y 0 = 0 ⇒ Phương trình tiếp tuyến:
y = − 1 ( x + 2 ) ⇒ y = − x − 2
CM
20 tháng 2 2018
+ Gọi M(a; b) là toạ độ của tiếp điểm
Đạo hàm y ' = - 1 ( 2 x + 3 ) 2 < 0 ; ∀ x .
+ Do tam giác OAB cân tại O nên tiếp tuyến ∆ song song với đường thẳng y= -x (vì tiếp tuyến có hệ số góc âm).
Nghĩa là
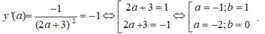
-Với a= -1; b= 1 phương trình ∆: y- 1= -( x+ 1) hay y= -x ( loại) .
-Với a= -2; b= 0 thì ∆ : y- 0= -( x+ 2) hay y=-x-2 (nhận).
Vậy phương trình tiếp tuyến cần tìm là y= -x- 2.
Chọn D.
CM
19 tháng 8 2018
Đáp án D
Phương pháp:
+) Viết phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ x o .
+) Tìm giao điểm của tiếp tuyến với các trục tọa độ.
+) Tính OA, OB, giải phương trình tìm x o → Phương trình tiếp tuyến và kết luận.
CM
25 tháng 5 2018
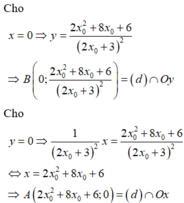
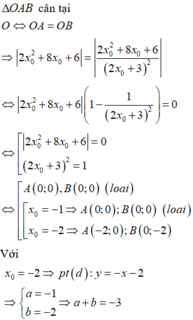
Chọn: D
Phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ x 0 là:
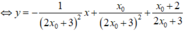
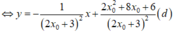
Cho x = 0
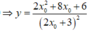
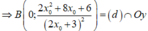
Cho y = 0
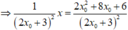
∆ O A B c â n t ạ i O ⇔ O A = O B
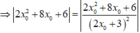
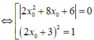
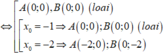
Với x 0 = - 2
