Chia số 120 thành bốn phần tỉ lệ với các số 2; 4; 6; 8. Các số đó theo thứ tự tăng dần là
A. 20 ; 40 ; 80 ; 100
B. 50 ; 40 ; 20 ; 10
C. 8 ; 16 ; 32 ; 40
D. 10 ; 20 ; 40 ; 50
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi 3 phần đó là a, b, c thì a+b+c = 120. Ta có:
a : b : c = 3 : 4 : 5 \(\Rightarrow\) \(\frac{a}{3}=\frac{b}{4}=\frac{c}{5}\).
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{a}{3}=\frac{b}{4}=\frac{c}{5}=\frac{a+b+c}{3+4+5}=\frac{120}{12}=10\)
Từ đó suy ra a = 10.3 = 30, b = 10.4 = 40, c = 10.5 = 50

a) gọi ba số a,b,c
theo dãy số dằng nhau ta có \(\frac{a}{2}\)=\(\frac{b}{3}\)=\(\frac{c}{4}\)=>\(\frac{a+b+c}{2+3+4}\)=\(\frac{99}{9}\)=11
=> a=22. b=33,c=44
b) tương tự gọi 3 số a,b,c,
theo dãy số dằng nhau ta có \(\frac{a}{3}\)=\(\frac{b}{3}\)=\(\frac{c}{4}\)=>\(\frac{a+b+c}{3+5+7}\)=\(\frac{285}{3+5+7}\)=19
=> a=57,b=95, c=133
c) tương tự bốn số là:\(\frac{247}{4}\);\(\frac{2717}{28}\);\(\frac{3211}{28}\);\(\frac{6175}{28}\)
d, tương tự : bốn số là 60; 105;120;180

X và Y và Z tỉ lệ thuận với 3;4 và 5
Ta có: x/3 = y/4 = z/5
= x - y + z / 3+4+5=20/12
x/3 = 20/12 => x

Giả sử 48 chia thành bốn phần là x; y; z; t tỉ lệ với các số 3; 5; 7; 9
Ta có: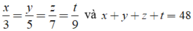
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
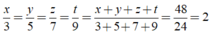
Do đó: x = 6; y = 10; z = 14; t = 18
Chọn đáp án D.

Gọi 4 số đó lần lượt là a,b,c,d.
Áp dụng dãy tỉ số bằng nhau ta có:
\(\frac{a}{7}=\frac{b}{11}=\frac{c}{13}=\frac{d}{25}=\frac{a+b+c+d}{7+11+13+25}=\frac{494}{56}=\frac{247}{28}\)
\(\Rightarrow\left\{{}\begin{matrix}\frac{a}{7}=\frac{247}{28}\Rightarrow a=\frac{247}{28}.7=\frac{247}{4}\\\frac{b}{11}=\frac{247}{28}\Rightarrow b=\frac{247}{28}.11=\frac{2717}{28}\\\frac{c}{13}=\frac{247}{28}\Rightarrow c=\frac{247}{28}.13=\frac{3211}{28}\\\frac{d}{25}=\frac{247}{28}.25\Rightarrow d=\frac{247}{28}.25=\frac{6175}{28}\end{matrix}\right.\)
Vậy ....
( Câu này bn có ghi sai đề không vậy??? Kết quả nó lớn quá.)
a, Gọi 3 số đó lần lượt là a, b, c.
Áp dụng dãy tỉ số bằng nhau ta có:
\(\frac{a}{2}=\frac{b}{3}=\frac{c}{4}=\frac{a+b+c}{2+3+4}=\frac{99}{9}=11\)
\(\Rightarrow\left\{{}\begin{matrix}\frac{a}{2}=11\Rightarrow a=11.2=22\\\frac{b}{3}=11\Rightarrow b=11.3=33\\\frac{c}{4}=11\Rightarrow c=11.4=44\end{matrix}\right.\)
Vậy số cần tìm lần lượt là : 22 ; 33 ; 44.

Gọi bốn số cần tìm là a,b,c,d
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{\dfrac{1}{2}}=\dfrac{b}{\dfrac{1}{5}}=\dfrac{c}{\dfrac{1}{7}}=\dfrac{d}{\dfrac{1}{14}}=\dfrac{a+b+c+d}{\dfrac{1}{2}+\dfrac{1}{5}+\dfrac{1}{7}+\dfrac{1}{14}}=\dfrac{128}{\dfrac{32}{35}}=140\)
Do đó: a=70; b=28; c=20; d=10
Vậy các số cần tìm sắp xếp theo thứ tự tăng dần là 10; 20; 40; 50
Đáp án cần chọn là: D