Phép chiếu hình bản đồ là cách biểu hiện mặt cong của địa cầu lên một mặt phẳng để mỗi điểm trên mặt cong tương ứng với
A. một điểm trên mặt phẳng
B. một điểm trên mặt cong
C. Ý A và B đúng
D. Ý A và B sai
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

tham khảo:
a) Vì M', N' tương ứng là hình chiếu của M, N trên mặt phẳng (P) nên hình chiếu của a trên mặt phẳng (P) là a’ đường thẳng đi qua hai điểm M', N'.
b) b vuông góc với M'N' và b vuông góc với MM' (do M' là hình chiếu của M trên (P)); M'N' cắt MM' tại M' do đó b vuông góc mặt phẳng tạo bởi M'N', MM' suy ra b có vuông góc với a.
c) b vuông góc với a và b vuông góc với MM' (do M' là hình chiếu của M trên (P)); a cắt MM' tại M do đó b vuông góc mặt phẳng tạo bởi a, MM' suy ra b có vuông góc với M'N'.

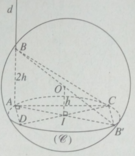
Ta có AH ⊥ DC. Do đó khi CD di động, điểm H luôn luôn nhìn đọan thẳng AI dưới một góc vuông. Vậy tập hợp các điểm H là đường tròn đường kính AI nằm trong mặt phẳng ( α ).

(H.90) Ta có hai hàm số tương ứng là: y = x 2 – 3x + 3 và y = x
Vậy
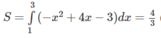

Ta có
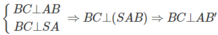
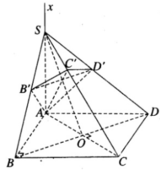
Ta lại có AB′ ⊥ SC nên suy ra AB′ ⊥ (SBC). Do đó AB′ ⊥ B′C
Chứng minh tương tự ta có AD′ ⊥ D′C.
Vậy ∠ ABC = ∠ AB′C = ∠ AC′C = ∠ AD′C = ∠ ADC = 90 °
Từ đó suy ra 7 điểm A, B, C, D, B’, C’, D’ cùng nằm trên mặt cầu đường kính là AC.

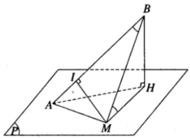
Giải sử ta có điểm M thuộc mặt phẳng (P) thỏa mãn các điều kiện của giả thiết đã cho. Gọi I là hình chiếu vuông góc của M trên AB. Hai tam giác vuông BIM và MHB bằng nhau vì có cạnh huyền chung và một cặp góc nhọn bằng nhau. Do đó MI = BH không đổi. Vậy điểm M luôn luôn nằm trên mặt trụ trục AB và có bán kính bằng BH.

| a. B, C là các điểm nằm trong mặt phẳng (P). | Đ |
| b, Mặt phẳng (P) chứa đựờng thắng AB | S |
| c. Đường thẳng l cắt AB ở điểm B | S |
| d. A,B,G là ba điểm cùng nằm trên một mặt phẳng | Đ |
| e. B,F và D là ba điểm thẳng hàng | S |
| f. B,C,E và D là bốn điểm cùng nằm trên một mặt phẳng | Đ |
Đáp án A