Nếu tam giác ABC có MN // BC (với M Є AB, N Є AC) thì
A. ΔAMN đồng dạng với ΔACB
B. ΔABC đồng dạng với MNA
C. ΔAMN đồng dạng với ΔABC
D. ΔABC đồng dạng với ΔANM
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Nếu Δ ABC = Δ A’B’C’ ta suy ra:
AB= A’B’, AC= A’C’, BC = B’C’
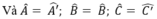
Theo định nghĩa hai tam giác đồng dạng, suy ra hai tam giác ABC và A’B’C’ đồng dạng với nhau

ta có : ΔABC~ΔDEF (gt)
=>\(\dfrac{AB}{DE}=\dfrac{AC}{DF}=\dfrac{BC}{\text{EF}}=k\)
=> DE = 3:2= 1,5 (cm)
DF = 4:2 = 2 (cm)
BC = 5:2 = 2,5 (cm )
=> Chu vi tam giác DEF = DE+DF+BC = 1,5+2+2,5 = 6(CM)
Ta có:
\(\dfrac{AB}{DE}=2;\dfrac{AC}{DF}=2;\dfrac{BC}{EF}=2\)
\(\Leftrightarrow\dfrac{3}{DE}=2;\dfrac{4}{DF}=2;\dfrac{5}{EF}=2\)
\(\Leftrightarrow DE=\dfrac{3}{2};DF=\dfrac{4}{2};EF=\dfrac{5}{2}\)
\(\Rightarrow C_{DEF}=\dfrac{3}{2}+\dfrac{4}{2}+\dfrac{5}{2}=\dfrac{12}{2}=6\left(cm\right)\)

ΔAHB vuông tại H có HI là đường cao
nên AI*AB=AH^2
ΔAHC vuông tại H có HK là đường cao
nên AK*AC=AH^2
=>AI*AB=AK*AC
=>AI/AC=AK/AB
=>ΔAIK đồng dạng với ΔACB

ΔA'B'C' 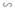 ΔA''B''C'' theo tỉ số đồng dạng k1 ⇒
ΔA''B''C'' theo tỉ số đồng dạng k1 ⇒ 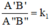
ΔA''B''C'' 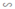 ΔABC theo tỉ số đồng dạng k2 ⇒
ΔABC theo tỉ số đồng dạng k2 ⇒ 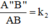
Mà ΔA'B'C' 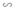 ΔA''B''C''; ΔA''B''C''
ΔA''B''C''; ΔA''B''C'' 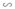 ΔABC
ΔABC
⇒ ΔA'B'C' 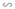 ΔABC (theo tính chất 3)
ΔABC (theo tính chất 3)
Tỉ số đồng dạng:
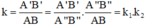
Vậy tam giác A'B'C' đồng dạng với tam giác ABC theo tỉ số k1.k2.

Vì tam giác ABC đồng dạng với tam giác DEF nên A ^ = D ^ = 80 ∘ , B ^ = E ^ = 70 ∘ , C ^ = F ^ = 30 ∘
Vậy C ^ = 30 ∘ là đúng
Đáp án: D
Vì MN // BC => tam giác AMN đồng dạng với tam giác ABC
Đáp án: C