Hình thoi có độ dài hai đường chéo là 15 cm và 20 cm. Tính độ dài đường cao của hình thoi
A. 12 cm
B. 7,5 cm
C. 15 cm
D. 24 cm
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
29 tháng 6 2023
a, Diện tích hình thoi:
(18 x 15):2= 135(cm2)
b, Chiều rộng HCN:
135:15= 9(cm)
Đáp số: a, 135cm2 ; b,9cm
8 tháng 11 2023
a, Diện tích hình thoi:
(18 x 15):2= 135(cm2)
b, Chiều rộng HCN:
135:15= 9(cm)
Đáp số: a, 135cm2 ; b,9cm
3 tháng 5 2017
Gọi hình thoi đó là ABCD
Hai đường chéo BD và AC cắt nhau và vuông góc tại O
Kẻ đường cao AH (H\(\in DC\))
a. SABCD=\(\dfrac{1}{2}.AC.BD=\dfrac{1}{2}.12.16=96\left(cm^2\right)\)
Vậy diện tích hình thoi đó là 96 cm2
b. Ta có: AO=OC=\(\dfrac{AC}{2}=\dfrac{12}{2}=6\left(cm\right)\)
OD=OB=\(\dfrac{BD}{2}=\dfrac{16}{2}=8\left(cm\right)\)
Xét \(\Delta DAO\) có \(\widehat{DOA}=90^o\)
=> OD2+AO2=AD2 (định lý Py-ta-go)
hay: 82+62=AD2
=> AD2=100
=> AD=10 (cm)
Vậy độ dài một cạnh của hình thoi đó là 10 cm
c. Ta có: SABCD=AH.DC
=> AH=\(\dfrac{S_{ABCD}}{DC}=\dfrac{96}{10}=9,6\left(cm\right)\)
Vậy độ dài đường cao của hình thoi đó là 9,6 cm
13 tháng 2 2020
Gọi hình thoi đó là \(ABCD\)
Hai đường chéo BD và AC cắt nhau và vuông góc tại O
Kẻ đường cao AH \(\left(H\in DC\right)\)
a ) \(S_{ABCD}=\frac{1}{2}.AC.BD=\frac{1}{2}.12.16=96\left(cm^2\right)\)
Vậy diện tích hình thoi đó là \(96cm^2\)
b ) Ta có : \(AO=OC=\frac{AC}{2}=\frac{12}{2}=6\left(cm\right)\)
\(OD=OB=\frac{BD}{2}=\frac{16}{2}=8\left(cm\right)\)
Xét \(\Delta DAO\)có \(\widehat{DOA}=90^0\)
\(\Rightarrow OD^2+AO^2=AD^2\)( định lí Py - ta - go )
Hay \(8^2+6^2=AD^2\)
\(\Rightarrow AD^2=100\)
\(\Rightarrow AD=10\left(cm\right)\)
Vậy độ dài một cạnh của hình thoi đó là 10 cm
c ) Ta có : \(S_{ABCD}=AH.DC\)
\(\Rightarrow AH=\frac{S_{ABCD}}{DC}=\frac{96}{10}=9,6\left(cm\right)\)
Vậy độ dài dduwowgf cao của hình thoi là 9,6 cm
Chúc bạn học tốt !!!
CM
1 tháng 8 2019
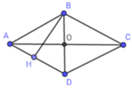
Giả sử hình thoi ABCD, đường chéo AC vuông góc với BD tại O, AC = 8 cm; BD = 6 cm.
Gọi BH là đường cao hình thoi kẻ từ đỉnh B.
Ta có: DO = 1 2 BD = 1 2 .6 = 3 (cm);
AO = 1 2 AC = 1 2 .8 = 4 (cm)
Áp dụng định lý Py-ta-go trong tam giác vuông AOD vuông tại O ta có:
AD = A O 2 + O D 2 = 4 2 + 3 2 = 5 (cm)
SABCD = 1 2 BD. AC = 1 2 6.8 = 24 (cm2)
SABCD = BH. AD => BH = S A B C D A D = 24 5 = 4, 8 (cm)
Đáp án cần chọn là: B
2 tháng 5 2021
Diện tích hình thoi là:
( 20 x 15 ) : 2 = 150 ( cm2 )
Đáp số : 150 cm2
PT
1
CM
17 tháng 10 2017
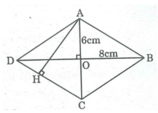
ABCD là hình thoi có O là giao điểm của hai đường chéo nên:
AO = OC = 6cm; OB = OD = 8cm
Trong tam giác vuông OAB, ta có:
A B 2 = O A 2 + O B 2 = 6 2 + 8 2 = 100
AB = 10 (cm)
Kẻ AH ⊥ CD (H ∈ CD)
Ta có: S A B C D = AH.CD ⇒ AH = S A B C D / CD = 96/10 = 9,6 (cm)
17 tháng 10 2021
Vì ABCD là hình thoi nên \(AB=BC=CD=DA=20\left(cm\right)\)
Và AC cắt BD tại O nên O là trung điểm AC,BD
\(\Rightarrow AC=2AO=32\left(cm\right);BD=2OB=24\left(cm\right)\)
Giả sử hình thoi ABCD, đường chéo AC vuông góc với BD tại O, AC = 20 cm; BD = 15 cm.
Gọi BH là đường cao hình thoi kẻ từ đỉnh B.
Ta có: DO = 1 2 BD = 1 2 .15 = 7,5 (cm);
AO = 1 2 AC = 1 2 .20 = 10 (cm)
Áp dụng định lý Py-ta-go trong tam giác vuông AOD vuông tại O ta có:
AD = A O 2 + O D 2 = 10 2 + 7 , 5 2 = 12,5 (cm)
SABCD = 1 2 BD. AC = 1 2 15.20 = 24 (cm2)
SABCD = BH. AD => BH = S A B C D A D = 150 12 , 5 = 12 (cm)
Đáp án cần chọn là: A