Chọn phát biểu đúng: Phương trình a x 2 + b x + c = 0 ( a ≠ 0 ) có hai nghiệm x 1 ; x 2 . Khi đó:
A. x 1 + x 2 = − b a x 1 . x 2 = c a
B. x 1 + x 2 = b a x 1 . x 2 = c a
C. x 1 + x 2 = − b a x 1 . x 2 = − c a
D. x 1 + x 2 = b a x 1 . x 2 = − c a
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mệnh đề \(P \Rightarrow Q\): “Nếu phương trình bậc hai \(a{x^2} + bx + c = 0\) có hai nghiệm phân biệt thì phương trình bậc hai \(a{x^2} + bx + c = 0\) có biệt thức \(\Delta = {b^2} - 4ac\;\, > 0\).”
Mệnh đề \(Q \Rightarrow P\): “Nếu phương trình bậc hai \(a{x^2} + bx + c = 0\) có biệt thức \(\Delta = {b^2} - 4ac\;\, > 0\) thì phương trình bậc hai \(a{x^2} + bx + c = 0\) có hai nghiệm phân biệt.”

Nghiệm chung x (nếu có) của hai phương trình là nghiệm của hệ:
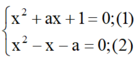
Lấy (1) trừ (2) vế trừ vế ta được:
ax + 1+ x+ a = 0
⇔ ( ax+ x) + (1+ a) =0
⇔ (a+ 1).x+ (1+ a) = 0
⇔ ( a+ 1) . (x+1)=0
⇔ a = - 1 hoặc x= -1
* Với a = -1 thay vào (2) ta được: x 2 - x + 1 = 0 phương trình này vô nghiệm
vì ∆ = ( - 1 ) 2 – 4 . 1 . 1 = - 3 < 0
nên loại a = -1.
*Thay x = -1 vào (2) suy ra a = 2.
Vậy với a = 2 thì phương trình có nghiệm chung là x = -1
Vậy chọn câu C.

Nghiệm chung x (nếu có) của hai phương trình là nghiệm của hệ:
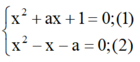
Lấy (1) trừ (2) vế trừ vế ta được:
ax + 1+ x+ a = 0
⇔ ( ax+ x) + (1+ a) =0
⇔ (a+ 1).x+ (1+ a) = 0
⇔ ( a+ 1) . (x+1)=0
⇔ a = - 1 hoặc x= -1
* Với a = -1 thay vào (2) ta được: x 2 - x + 1 = 0 phương trình này vô nghiệm
vì ∆ = ( - 1 ) 2 – 4 . 1 . 1 = - 3 < 0
nên loại a = -1.
*Thay x = -1 vào (2) suy ra a = 2.
Vậy với a = 2 thì phương trình có nghiệm chung là x = -1
Vậy chọn câu C.

Đáp án A
Cho phương trình bậc hai a x 2 + bx + c (a ≠ 0).
Nếu x 1 ; x 2 là hai nghiệm của phương trình thì:
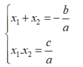

Đáp án A
Cho phương trình bậc hai a x 2 + b x + c ( a ≠ 0 ) .
Nếu x 1 ; x 2 là hai nghiệm của phương trình thì:
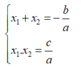

a. Đúng
Vì x 2 + 1 > 0 với mọi x nên phương trình đã cho tương đương với phương trình:
4x – 8 + (4 – 2x) = 0 ⇔ 2x – 4 = 0 ⇔ 2x = 4 ⇔ x = 2
b. Đúng
Vì x 2 – x + 1 = x - 1 / 2 2 + 3/4 > 0 với mọi x nên phương trình đã cho tương đương với phương trình:
(x + 2)(2x – 1) – x – 2 = 0 ⇔ (x + 2)(2x – 2) = 0
⇔ x + 2 = 0 hoặc 2x – 2 = 0 ⇔ x = - 2 hoặc x = 1
c. Sai
Vì điều kiện xác định của phương trình là x + 1 ≠ 0 ⇔ x ≠ - 1
Do vậy phương trình  không thể có nghiệm x = - 1
không thể có nghiệm x = - 1
d. Sai
Vì điều kiện xác định của phương trình là x ≠ 0
Do vậy x = 0 không phải là nghiệm của phương trình 

a.
\(f\left(x\right)=0\) có nghiệm \(x=1\Rightarrow f\left(1\right)=0\)
\(\Rightarrow1-2\left(m-2\right)+m+10=0\)
\(\Rightarrow m=15\)
Khi đó nghiệm còn lại là: \(x_2=\dfrac{m+10}{x_1}=\dfrac{25}{1}=25\)
b.
Pt có nghiệm kép khi: \(\Delta'=\left(m-2\right)^2-\left(m+10\right)=0\)
\(\Rightarrow m^2-5m-6=0\Rightarrow\left[{}\begin{matrix}m=-1\\m=6\end{matrix}\right.\)
Với \(m=-1\) nghiệm kép là: \(x=-\dfrac{b}{2a}=m-2=-3\)
Với \(m=6\) nghiệm kép là: \(x=-\dfrac{b}{2a}=m-2=4\)
c.
Pt có 2 nghiệm âm pb khi:
\(\left\{{}\begin{matrix}\Delta'=m^2-5m-6>0\\x_1+x_2=2\left(m-2\right)< 0\\x_1x_2=m+10>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}m< -1\\m>6\end{matrix}\right.\\m< 2\\m>-10\end{matrix}\right.\) \(\Rightarrow-10< m< -1\)
d.
\(f\left(x\right)< 0;\forall x\in R\Rightarrow\left\{{}\begin{matrix}a=1< 0\left(\text{vô lý}\right)\\\Delta'=m^2-5m-6< 0\end{matrix}\right.\)
Không tồn tại m thỏa mãn
Cho phương trình bậc hai a x 2 + b x + c = 0 ( a ≠ 0 ) . Nếu x 1 ; x 2 là hai nghiệm của phương trình thì x 1 + x 2 = − b a x 1 . x 2 = c a
Đáp án: A