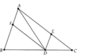
1. Cho tam giác ABC có AD là phân giác (AD thuộc BC). Qua D kẻ đường thẳng song song với AB, cắt AC tại E. Qua E kẻ đường thẳng song song với BC, cắt AB tại K. Chứng Minh:
a) Tam giác AED là tam giác cân
b) AE = BK
2.Trên cạnh huyền BC của tam giác vuông ABC, lấy các điểm D và E sao cho BD = BA, CE = CA. Tính DAE
Các bạn làm ơn giải bài toán rõ ràng đừng ghi câu hỏi tương tự