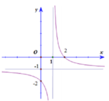
Cho hàm số y = a x + b x + c có đồ thị như hình vẽ, a, b, c là các số nguyên. Tính giá trị của biểu thức T = a – 3b + 2c
A. T = – 9
B. T = – 7
C. T = 12
D. T = 10
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Dựa vào đồ thị hàm số ta thấy:
Đồ thị hàm số có TCĐ và TCN là
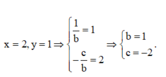
Đồ thị hàm số đi qua điểm có tọa độ ( -2; 0) nên a= -2
Suy ra A= a+ b+ c= -2+ 1+ ( -2) = -3
Chọn B.

Đáp án A
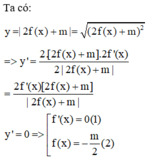
Bài toán cần 5 điểm cực trị => Tổng số nghiệm của (1) và (2) phải là 5
Đối với (1) => số nghiệm chính là số điểm cực trị. Nhìn vào đồ thị => có 3 cực trị
=> Phương trinh (2) phải có 2 nghiệm khác 3 nghiệm trên. Nhìn vào đồ thị ta thấy
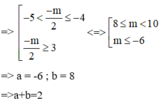

Chọn D
Từ đồ thị hàm số, ta suy ra
Đồ thị hàm số có tiệm cận đứng là đường thẳng x = 1, tiệm cận ngang là đường thẳng y = -1
Đồ thị hàm số đi qua các điểm A(2;0), B(0;-2)
Từ biểu thức hàm số y = a x + b x + c (vì đồ thị hàm số là đồ thị hàm nhất biến nên ac - b ≠ 0), ta suy ra
Đồ thị hàm số có tiệm cận đứng là đường thẳng x = -c, tiệm cận ngang là đường thẳng y = a.
Đồ thị hàm số đi qua ![]()
Đối chiếu lại, ta suy ra c = -1, a = -1, b
Vậy ![]()

Đáp án B
Đặt t = 2 sin x 2 ≥ t ≥ 0 dựa vào đường tròn lượng giác ta thấy:
Với t ∈ 0 ; 2 một giá trị của t có 6 giá trị của x
Với t = 2 một giá trị của t có 3 giá trị của x
Với t = 0 một giá trị của t có 4 giá trị của x
Dựa vào đồ thị ta thấy rằng PT f 2 sin x = f m có 12 nghiệm phân biệt ⇔ P T : f t = f m
có 2 nghiệm phân biệt thuộc khoảng 0 ; 2 ⇔ f m ∈ − 27 16 ; 0 ⇔ m ∈ 0 ; 2 ⇒ T = 4
Đáp án A
Phương pháp: Dựa vào các đường tiệm cận và các điểm đi qua của đồ thị hàm số.
Cách giải:
Đồ thị hàm số y = a x + b x + c có đường TCĐ x = – c => – c = 1 <=> c = – 1, TCN y = a => a = –1
Đồ thị hàm số đi qua (0;–1)