Trong không gian xét m → , n → , p → , q → là những vectơ đơn vị (có độ dài bằng 1). Gọi M là giá trị lớn nhất của biểu thức 0 m → - n → 2 + m → - p → 2 + m → - q → 2 + n → - p → 2 + n → - q → 2 + p → - q → 2 . Khi đó M - M thuộc khoảng nào sau đây ?
A. 4 ; 13 2
B. 7 ; 19 2
C. (17;22)
D. (10;15)


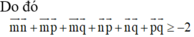
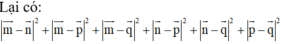



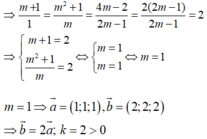
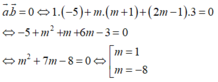
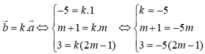




Đáp án D
Ta có: 0 ≤ m → + n → + p → + q → 2 = 4 + 2 m → n → + m → p → + m → q → + n → p → + n → q → + p → q →
Do đó m → n → + m → p → + m → q → + n → p → + n → q → + p → q → ≥ - 2
Lại có: m → - n → 2 + m → - p → 2 + m → - q → 2 + n → - p → 2 + n → - q → 2 + p → - q → 2
= 3 m → 2 + n → 2 + p → 2 + q → 2 - 2 m → n → + m → p → + m → q → + n → p → + n → q → + p → q → ≤ 12 - 2( - 2) = 16
Vậy M = 16 => M - M = 12