Cho hình lăng trụ đứng ABC.A'B'C' có AB = 5cm, AC = 13cm, BC = 12cm và đường cao AA’ = 8cm. Diện tích toàn phần của lăng trụ là
A. 220 cm2;
B. 180 cm2;
C. 270 cm2;
D. 300 cm2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét tam giác ABC có nửa chu vi của tam giác là:
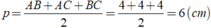
Khi đó ta có
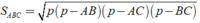

+ Diện tích xung quanh của hình lăng trụ


Lời giải:
$AC=\sqrt{BC^2-AB^2}=\sqrt{20^2-16^2}=12$ (cm)
Diện tích đáy là: $(12.16):2=96$ (cm2)
Diện tích toàn phần:
$S=p_{đáy}.h+2S_{đáy}=(16+12+20).12+2.96=768$ (cm2)
Thể tích lăng trụ:
$V=S_{đáy}.h=96.12=1152$ (cm3)

\(S_{XQ}=\left(5+12+13\right)\cdot8=8\cdot26=204\left(cm^2\right)\)
\(S_{TP}=204+2\cdot5\cdot12\cdot2=204+4\cdot60=204+240=444\left(cm^2\right)\)
\(V=5\cdot12\cdot8=60\cdot8=480\left(cm^3\right)\)

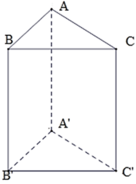
Ta có: A B 2 + A C 2 = B C 2 ⇒ Δ ABC vuông tại A.
Do đó: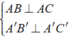
Vì AC vuông góc với hai đường thẳng cắt nhau là AB và AA'
Nên AC ⊥ ( ABB'A' )
Vậy có 3 mặt phẳng vuông góc với ( ABB'A' ) là:
( ABC ), ( A'B'C' ),( ACC'A' )
Chọn đáp án D.
Đáp án D