Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Xét (O) có
CM,CA là tiếp tuyến
=>CM=CA và OC là phân giác của góc MOA(1)
Xét (O) có
DM,DB là tiếp tuyến
=>DM=DB và OD là phân giác của góc MOB(2)
Từ (1), (2) suy ra góc COD=1/2*góc AOB=90 độ
=>O nằm trên (I)
Xét hình thang ABDC có
O,I lần lượt là trung điểm của AB,CD
=>OI là đường trung bình
=>OI//AC//BD
=>OI vuông góc AB
=>AB tiếp xúc (I) tại O

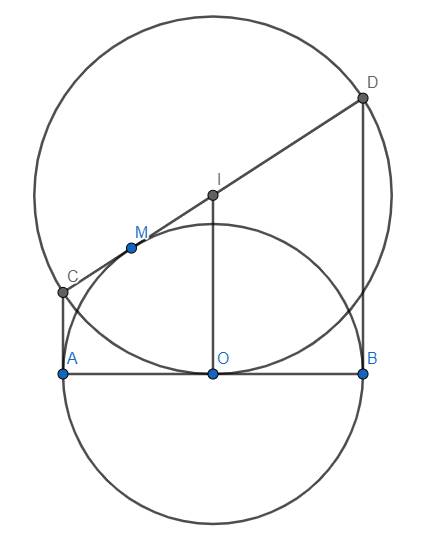
Dễ thấy ABDC là hình thang. Vì O, I lần lượt là trung điểm của AB, CD nên OI là đường trung bình của hình thang ABDC.
\(\Rightarrow\left\{{}\begin{matrix}OI//AC//BD\Rightarrow OI\perp AB\left(tạiO\right)\\OI=\dfrac{AC+BD}{2}=\dfrac{CM+DM}{2}=\dfrac{CD}{2}=R\end{matrix}\right.\) với R là bán kính của đường tròn \(\left(CD\right)\).
Từ đó suy ra AB tiếp xúc (I) tại O. (đpcm)

Có \(\widehat{CAO}=\widehat{CMO}=90^o\) nên \(A,M\) cùng nhìn \(CO\) dưới góc vuông do đó \(C,M,O,A\) cùng thuộc một đường tròn.