cho hình thoi ABCD. Gọi I là giao điểm của các đường trung trức của AB và CD. Gọi J là giao điểm cả 2 đường trung Trực của AB và CB. CM AICJ là hình thoi
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
28 tháng 7 2021
a) Xét ΔADE vuông tại E và ΔBCF vuông tại F có
AD=BC(ABCD là hình thang cân)
\(\widehat{ADE}=\widehat{BCF}\)(ABCD là hình thang cân)
Do đó: ΔADE=ΔBCF(Cạnh huyền-góc nhọn)
Suy ra: DE=CF(Hai cạnh tương ứng)
b) Xét ΔADB và ΔBCA có
AD=BC(ABCD là hình thang cân)
AB chung
DB=CA(ABCD là hình thang cân)
Do đó: ΔADB=ΔBCA(c-c-c)
Suy ra: \(\widehat{DBA}=\widehat{CAB}\)(hai góc tương ứng)
hay \(\widehat{IAB}=\widehat{IBA}\)
Xét ΔIAB có \(\widehat{IAB}=\widehat{IBA}\)(cmt)
nên ΔIAB cân tại I(Định lí đảo của tam giác cân)
Suy ra: IA=IB
28 tháng 7 2021
c) Ta có: \(\widehat{OAB}=\widehat{ODC}\)(hai góc đồng vị, AB//CD)
\(\widehat{OBA}=\widehat{OCD}\)(hai góc đồng vị, AB//CD)
mà \(\widehat{ODC}=\widehat{OCD}\)(ABCD là hình thang cân)
nên \(\widehat{OAB}=\widehat{OBA}\)
Xét ΔOAB có \(\widehat{OAB}=\widehat{OBA}\)(cmt)
nên ΔOAB cân tại O(Định lí đảo của tam giác cân)
Suy ra: OA=OB
Ta có: OA+AD=OD(A nằm giữa O và D)
OB+BC=OC(B nằm giữa O và C)
mà OA=OB(cmt)
và AD=BC(ABCD là hình thang cân)
nên OD=OC
Ta có: IA+IC=AC(I nằm giữa A và C)
IB+ID=BD(I nằm giữa B và D)
mà IA=IB(cmt)
và AC=BD(cmt)
nên IC=ID
Ta có: OA=OB(cmt)
nên O nằm trên đường trung trực của AB(1)
Ta có: IA=IB(cmt)
nên I nằm trên đường trung trực của AB(2)
Ta có: OD=OC(cmt)
nên O nằm trên đường trung trực của DC(3)
Ta có: ID=IC(cmt)
nên I nằm trên đường trung trực của DC(4)
Từ (1) và (2) suy ra OI là đường trung trực của AB
Từ (3) và (4) suy ra OI là đường trung trực của DC
7 tháng 7 2023
a: góc OAB=góc ADC
góc OBA=góc BCD
mà góc ADC=góc BCD
nên góc OAB=góc OBA
=>OA=OB
OA+AD=OD
OB+BC=OC
mà OA=OB và AD=BC
nên OD=OC
b: Xét ΔABD và ΔBAC có
AB chung
BD=AC
AD=BC
=>ΔABD=ΔBAC
=>góc IAB=góc IBA
=>IA=IB
=>IC=ID
OA=OB và IA=IB
=>OI là trung trực của AB
OC=OD
IC=ID
=>OI là trung trực của CD
7 tháng 1 2023
a: Xét ΔOAN và ΔOCK có
góc OAN=góc OCK
góc AON=góc COK
Do đó: ΔOAN đồng dạng với ΔOCK
=>OA/OC=NA/CK
Xét ΔNBO và ΔKDO có
góc NBO=góc KDO
góc BON=góc DOK
Do đo: ΔNBO đồng dạng với ΔKDO
=>OB/OD=BN/KD
OA/OC=NA/CK
mà OB/OD=OA/OC
nên BN/KD=NA/CK
=>BN*CK=KD*NA
b: Xét ΔNDK có AN//DK
nên AN/DK=MN/MK
Xét ΔMKC có BN//KC
nên BN/KC=MN/MK
=>AN/DK=BN/DC
mà NA/CK=BN/KD
nên DK/DC=CK/KD=1
=>DK=KC
=>K là trung điểm của CD
T
24 tháng 4 2017
a, xét tam giác NPA và tam giác CBP có
AP=PB ; goc APN= goc CPB ; goc PAN = goc PBC (ND//BC)
==> tam giác APN = tam giác BPC ( g.c.g)
b. vì ÁP//DC ==> tam giác NPA đồng dạng với NCD
mà tam giác NPA đồng dạng với tam giác CPB
==> tam giác CPB đồng dạng với tam giác NCD
CM
7 tháng 1 2017
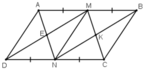
ABCD là hình bình hành ⇒ AB = CD.
M là trung điểm AB ⇒ AM = MB = AB/2.
N là trung điểm CD ⇒ CN = DN = CD/2.
⇒ AM = MB = CN = DN.
+ Tứ giác BMDN có: BM // DN và BM = DN
⇒ BMDN là hình bình hành
⇒ DM // BN hay ME // NK
+ Tứ giác AMCN có: AM // NC, AM = NC
⇒ AMCN là hình bình hành
⇒ AN // CM hay EN // MK.
+ Tứ giác MENK có: ME // NK và NE // MK
⇒ MENK là hình bình hành.
a) MENK là hình thoi
⇔ MN ⊥ EK.
⇔ CD ⊥ AD (Vì EK // CD và MN // AD)
⇔ ABCD là hình chữ nhật.
b) MENK là hình chữ nhật
⇔ MN = EK
Mà MN = BC;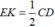 
(vì tam giác MCD có E và K lần lượt là trung điểm MD, MC nên EK là đường trung bình của tam giác MCD).
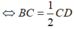
⇔ CD = 2.BC.
c) MENK là hình vuông
⇔ MENK là hình thoi và đồng thời là hình chữ nhật
⇔ ABCD là hình chữ nhật và có CD = 2.BC.