Cho lục giác đều ABCDEF. Chứng minh:
a) tam giác ACE là tam giác đều
b) tứ giác ABDE là hình chữ nhật
c) AD,BE và CF đồng quy tại trung điểm I của mỗi đường
d) tam giác AIB là tam giác đều
e) AD vuông góc với EC
f) tứ giác AICB là hình thoi
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
16 tháng 12 2022
a: Xét ΔCAB có CD/CB=CE/CA
nên DE//AB và DE=AB/2
=>DF//AB và DF=AB
=>ABDF là hình bình hành
Xét tứ giác ABDE có DE//AB
nên ABDE là hình thang
b: Xét tứ giác ADCF có
E là trug điểm chung của AC và DF
góc ADC=90 độ
Do đo: ADCF là hình chữ nhật
c: Vì ABDF là hình bình hành
nên AD cắt BF tại trung điểm của mỗi đường
=>B,I,F thẳng hàng
15 tháng 7 2021
a) Xét ΔABC vuông tại A và ΔHAC vuông tại H có
\(\widehat{C}\) chung
Do đó: ΔABC\(\sim\)ΔHAC(g-g)
b) Xét tứ giác AKHI có
\(\widehat{KAI}=90^0\)
\(\widehat{HIA}=90^0\)
\(\widehat{HKA}=90^0\)
Do đó: AKHI là hình chữ nhật(Dấu hiệu nhận biết hình chữ nhật)
c) Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHB vuông tại H có HI là đường cao ứng với cạnh huyền AB, ta được:
\(AI\cdot AB=AH^2\)(1)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHC vuông tại H có HK là đường cao ứng với cạnh huyền AC, ta được:
\(AK\cdot AC=AH^2\)(2)
Từ (1) và (2) suy ra \(AI\cdot AB=AK\cdot AC\)
25 tháng 2 2023
a: Xét tứ giác BFEC có
góc BFC=góc BEC=90 độ
=>BFEC nội tiếp
=>góc BFE+góc BCE=180 độ
=>góc AFE=góc ACB
mà góc FAE chung
nên ΔAFE đồng dạng với ΔACB
b: Xét tứ giác BFHD có
góc BFH+goc BDH=180 độ
=>BFHD là tứ giác nội tiếp
Xét tứ giác CEHD có
góc CEH+góc CDH=180 độ
=>CEHD là tứ giác nội tiếp
góc FDH=góc FBH
góc EDH=góc ACF
mà góc FBH=góc ACF
nên góc FDH=góc EDH
=>DH là phân giác của góc FDE(1)
góc EFH=góc CAD
góc DFH=góc EBC
mà góc CAD=góc EBC
nên góc EFH=góc DFH
=>FH là phân giác của góc EFD(2)
Từ (1), (2) suy ra H là giao của ba đường phân giác của ΔDEF
c: Xét ΔBHD vuông tại D và ΔBCE vuông tại E có
góc HBD chung
=>ΔBHD đồg dạng với ΔBCE
=>BH/BC=BD/BE
=>BH*BE=BC*BD
Xét ΔCDH vuông tại Dvà ΔCFB vuông tại F có
góc FCB chung
=>ΔCDH đồng dạng với ΔCFB
=>CD/CF=CH/CB
=>CD*CB=CH*CF
=>BH*BE+CH*CF=BC^2
CM
26 tháng 8 2017
Đáp án B
 |
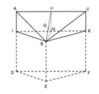Góc giữa mặt phẳng (ABC) và (DEF) bằng với góc giữa 2 mặt phẳng (ABC) và (BIK) trong đó mặt phẳng (BIK) song song với (DEF)
Vẽ đường cao BH của tam giác đều ABC, suy ra H là trung điểm AC và BH = a 3 2
Gọi M là trung điểm IK. Khi đó HM là đường trung bình của hình chữ nhật AIKC
HM =AI = a 2 và HM song song với AI
Trong mặt phẳng (BHM) vẽ MG ⊥ BH tại G
Do MG ⊥ BH và AC ⊥ MG(AC ⊥ (BHM)) nên MG ⊥ (ABC) (2)
Từ (1) và (2) => góc giữa 2 mặt phẳng (ABC) và (BKI) bằng góc giữa MG với HM, tức góc HMG
Trong ∆ B H M vuông tại M, ta có:
CM
9 tháng 9 2019
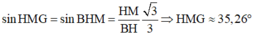
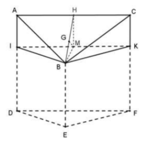
Vẽ đường cao BH của tam giác đều ABC, suy ra H là trung điểm AC và B H = 3 2 a
Gọi M là trung điểm IK. Khi đó HM là đường trung bình của hình chữ nhật AIKC
Chọn B
18 tháng 3 2023
a: Xét ΔAIB vuông tại I và ΔAEC vuông tại E có
góc IAB chung
=>ΔAIB đồng dạng vơi ΔAEC
b: ΔAIB đồng dạng với ΔAEC
=>AI/AE=AB/AC
=>AI/AB=AE/AC
=>ΔAIE đồng dạng với ΔABC và AB*AE=AI*AC
c: Xét ΔFAC vuông tại F và ΔICB vuông tại I có
góc FAC=góc ICB
=>ΔFAC đồng dạng với ΔICB
=>AF/IC=CA/CB
=>AF*CB=CA*IC
=>AB*AE+AF*CB=AC^2
28 tháng 3 2020
Gọi M là trung điểm BC ; N là điểm đối xứng với H qua M.
M là trung điểm của BC và HN nên BNCH là hình bình hành
\(\Rightarrow NC//BH\)
Mà \(BH\perp AC\Rightarrow NC\perp AC\)hay AN là đường kính của đường tròn ( O )
Dễ thấy OM là đường trung bình \(\Delta AHN\) suy ra \(OM=\frac{1}{2}AH\)
M là trung điểm BC nên OM \(\perp\)BC
Xét \(\Delta AHG\)và \(\Delta OGM\)có :
\(\widehat{HAG}=\widehat{GMO}\); \(\frac{GM}{GA}=\frac{OM}{HA}=\frac{1}{2}\)
\(\Rightarrow\Delta AGH~\Delta MOG\left(c.g.c\right)\Rightarrow\widehat{AGH}=\widehat{MGO}\)hay H,G,O thẳng hàng
28 tháng 3 2020
gọi E,F,T lần lượt là trung điểm của AB,CD,BD
Đường thẳng ME cắt NF tại S
Vì AC = BD \(\Rightarrow EQFP\)là hình thoi \(\Rightarrow EF\perp PQ\)( 1 )
Xét \(\Delta TPQ\)và \(\Delta SEF\)có : \(ME\perp AB,TP//AB\)
Tương tự , \(NF\perp CD;\)\(TQ//CD\)
\(\Rightarrow\Delta TPQ~\Delta SEF\)( Góc có cạnh tương ứng vuông góc )
\(\Rightarrow\frac{SE}{SF}=\frac{TP}{TQ}=\frac{AB}{CD}\)
Mặt khác : \(\Delta MAB~\Delta NCD\Rightarrow\frac{AB}{CD}=\frac{ME}{NF}\)( tỉ số đường cao = tỉ số đồng dạng )
Suy ra : \(\frac{ME}{NF}=\frac{SE}{SF}\)\(\Rightarrow EF//MN\)( 2 )
Từ ( 1 ) và ( 2 ) suy ra \(MN\perp PQ\)