Hãy tìm dạng lượng giác của các số phức: z−; -z;1/z;kz (k ∈R^*) trong mỗi trường hợp sau:
a) z=r(cosφ+isin φ)(r>0)
b) z=1+i √3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D.
Ta có phương trình đã cho tương đương với phương trình:
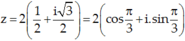
Do đó: 
Suy ra: ![]()
Vậy số phức w = (1 + i )z5 có phần thực là ![]() và phần ảo là
và phần ảo là ![]()
Tổng của phần thực và phần ảo là 32.
a) \(\overline{z}=r\left(\cos\left(-\phi\right)+i\sin\left(-\phi\right)\right)\)
\(-z=r\left(\cos\left(\phi+\pi\right)+isin\left(\phi+\pi\right)\right)\)
\(\frac{1}{\overline{z}}=\frac{1}{\overline{zz}}z=\frac{1}{\left|z\right|^2}z=\frac{1}{r}\left(\cos\phi+i\sin\phi\right)\)
\(kz=kr\left(\cos\phi+i\sin\phi\right)\)khi k>0
\(kz=-kr\left(\cos\left(\phi+\pi\right)+i\sin\left(\phi+\pi\right)\right)\)khi k<0
b) \(z=1+i\sqrt{3}=2\left(\cos\frac{\pi}{3}+i\sin\frac{\pi}{3}\right)\)
\(-z=2\left(\cos\frac{4\pi}{3}+i\sin\frac{4\pi}{3}\right)\)
\(\frac{1}{\overline{z}}=\frac{1}{2}\left(\cos\frac{\pi}{3}+i\sin\frac{\pi}{3}\right)\)
\(kz=2k\left(\cos\frac{\pi}{3}+i\sin\frac{\pi}{3}\right)\)nếu k>0
\(kz=-2k\left(\cos\frac{4\pi}{3}+i\sin\frac{4\pi}{3}\right)\)nếu k<0
LAI MAY NUA CO VAN DE VE QUANG HOC THAT ROI