tính tổng
1/(3(√1+√2))+1/(5(√2+√3)+.................+1/(97(√48+√49))
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

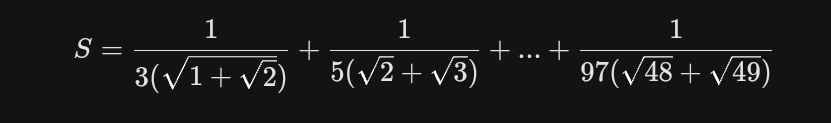

mức trung bình của năm số tự nhiên khác nhau là 4 nếu sự khác nhau giữa lớn nhất và nhỏ hơn của những con số này là càng lớn càng tốt với mức trung bình của số cây khác là những gì


a,
Đặt A=99-97+95-93+91-89+...+7-5+3-1
A={99-97}+{95-93}+{91-89}+...+{3-1}
A=2 + 2 + 2 +...+ 2 có 25 chữ số 2
A=2.25
A=50
Đúng 100/100 luôn đó cho minh nhá
a) Ta có: 99-97+95-93+91-89+...+7-5+3-1=
=(99-97)+(95-93)+(91-89)+...+(7-5)+(3-1)=
= 2+2+2+...+2+2 (25 số 2)=2.25=50

a) 99 - 97 + 95 - 93 + 91 - 89 +.....+ 7 - 5 + 3 - 1
= (99 - 97) + (95 - 93) + (91 - 89) +.... + (7 - 5) + ( 3 - 1)
= 2 + 2 + .... + 2
= 2 x 25 = 50
Vậy giá trị biểu thức là 50
b) 50 - 49 + 48 - 47 + 46 - 45 + ..... + 4 - 3 + 2 - 1
= (50 - 49) + (48 - 47) +......+(4 - 3) + (2 - 1)
= 1 + 1 +.....+ 1 + 1
= 1 x 25 = 25
Vậy giá trị biểu thức là 25

a) A=(3+7+...+99)- (1+5+...+97)
ta tính tổng các dãy số theo công thức: số số hạng: ( số cuối- số đầu) : khoảng cách +1
tổng = (số đầu+ cuối). số số hạng :2
=> (3+7+...+99)= \(\frac{\left(99+3\right).\left[\left(99-3\right):4+1\right]}{2}=\frac{102.25}{2}=1275\)
(1+5+...+97)= \(\frac{\left(1+97\right).\left[\left(97-1\right):4+1\right]}{2}=1225\)
=> A=1275-1225=50
tương tự làm câu B nha

satoshi
Có phải dòng đầu tiên bạn thiếu dấu "..." đúng không nhỉ???
a, 1+ \((\)- 2 \()\)+ 3 + \((\)- 4\()\)+ 19 + \((\)- 20 \()\)
= 1 - 2 + 3 - 4 + 19 - 20
= 20 - 19 + 4 - 3 + 2 - 1
= 1 + 4 - 3 + 2 - 1
= 1 + 1 + 2 - 1
= 1 + 1 + 1
= 3
c, 2 - 4 + 6 - 8 +....+ 48 -50
đặt A = 2 - 4 + 6 - 8 +....+ 48 -50
= -2 + -2 + -2 +.....+ -2 \((\) lưu ý : mỗi số -2 có đóng mở ngoặc và có 50 : 2 = 25 chữ số -2 \()\)
= 25 \(_{\times}\) -2
= - 50

cái này bạn mở sách bồi dưỡng toán ra trang gần cuối là thấy ngay ấy mà

So sánh tổng : S = 1/5 + 1/9 + 1/10 + 1/41 + 1/42 với 1/2
S=
=50/50+50/49+50/48+...+50/2
=50.(1/50+1/49+1/48+...+1/4+1/3+1/2)
=50
P=
P=(1/49+1)+(2/48+1)+...+(48/2+1)+1
P= 50/49+50/48+....+50/2+50/50=1
vậy s/p = 1/50