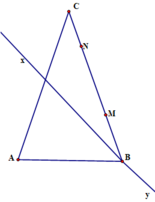
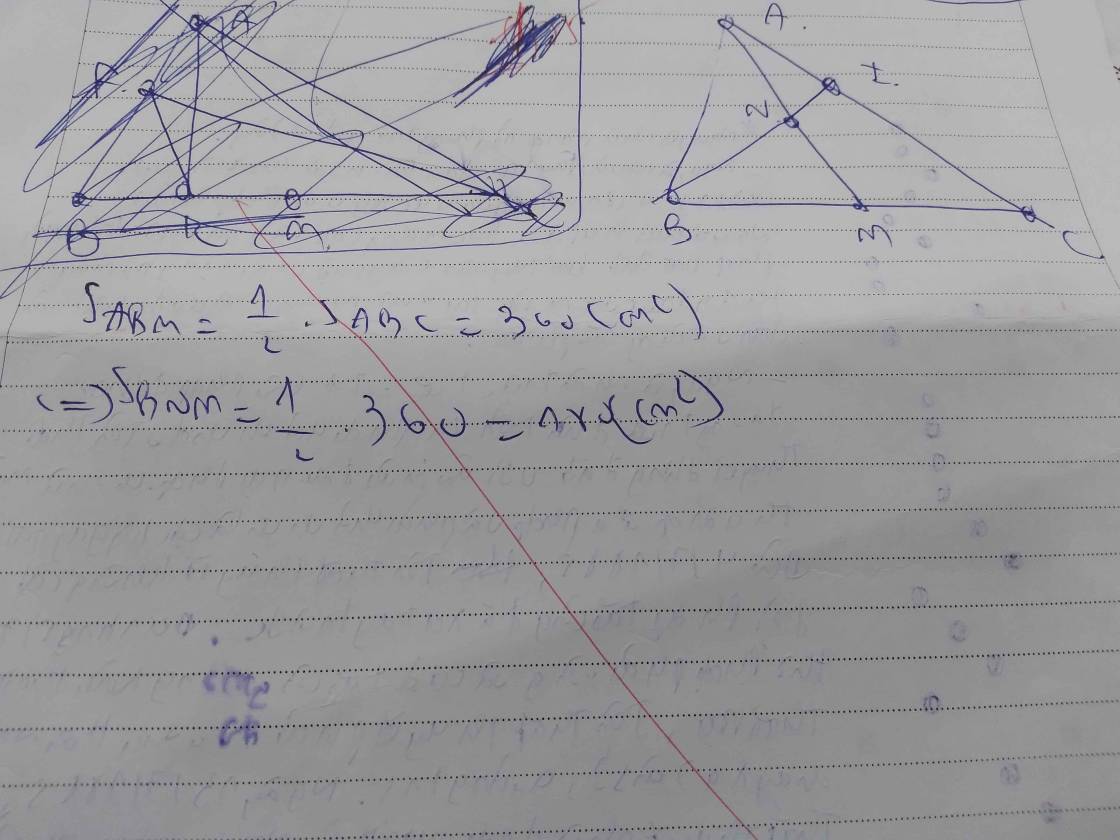
Cho tam giác abc có ba =bc m và n là hai điểm chính giữa của ba và bc
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


4) Gọi P, Q lần lượt là tâm của các đường tròn ngoại tiếp tam giác MBK, tam giác MCK và E là trung điểm của đoạn PQ. Vẽ đường kính ND của đường tròn (O) . Chứng minh ba điểm D, E, K thẳng hàng.

Vì N là điểm chính giữa cung nhỏ BC nên DN là trung trực của BC nên DN là phân giác B D C ^
Ta có K Q C ^ = 2 K M C ^ (góc nọi tiếp bằng nửa góc ở tâm trong dường tròn (Q))
N D C ^ = K M C ^ (góc nội tiếp cùng chắn cung N C ⏜ )
Mà B D C ^ = 2 N D C ^ ⇒ K Q C ^ = B D C ^
Xét 2 tam giác BDC & KQC là các các tam giác vuông tại D và Q có hai góc ở ⇒ B C D ^ = B C Q ^ do vậy D, Q, C thẳng hàng nên KQ//PK
Chứng minh tương tự ta có ta có D, P, B thẳng hàng và DQ//PK
Do đó tứ giác PDQK là hình bình hành nên E là trung điểm của PQ cũng là trung điểm của DK. Vậy D, E, K thẳng hàng (điều phải chứng minh).

Đáp án+Giải thích các bước giải:
Diện tích tam giác bằng diện tích tam giác do chung chiều cao từ , đáy
Do đó diện tích là:
Diện tích tam giác bằng diện tích tam giác do chung chiều cao từ , đáy
Do đó diện tích là:
Nối với
Diện tích tam giác bằng diện tích tam giác do chung chiều cao từ , đáy
Diện tích tam giác bằng diện tích tam giác do chung chiều cao từ , đáy
Diện tích tam giác Diện tích tam giác Diện tích tam giác
lần Diện tích tam giác
Hay Diện tích tam giác lần Diện tích tam giác
Do đó chiều cao từ xuống đáy của tam giác bằng bằng hai lần chiều cao từ xuống của tam giác
Đó cũng là chiều cao của tam giác và , đáy chung nên diện tích tam giác bằng hai lần diện tích tam giác . Hai tam giác này lại có chung chiều cao từ xuống nên đáy bằng nửa đáy

Cho P là giao điểm của ba đường phân giác trong của tam giác ABC. Đường thẳng qua P và vuông góc với CP cắt các tia CA, CB tại M, N. Chứng minh rằng:
a) Điểm M nằm giữa hai điểm C và A, điểm N nằm giữa hai điểm C và B.
b)
c) AP2.BC+BP2.AC+CP2.AB=AB.AC.BC
phần b đây các bạn

VẼ HÌNH (đề câu b sai ;Gọi _D_ là giao điểm của hai tia BA và ME .......... MỚI ĐÚNG )
___a) Xét tam giác BEA và tam giác BEM ,co :
BE la canh chung
BA=BM (gia thiet) (1)
gocABE = gocMBE (vi BE la tia phan giac cua gocABC)
Do đo : tam giác BEA = tam giác BEM (c-g-c)
=> gocBME=gocBAE=90do (2 góc tương ứng)
=> EM vuông góc với BC
___b) Xet :tam giác ADE và tam giác MCE ,co :
góc A = góc M = 90do (cmt)
gócAED=gocMEC( 2 góc đối đỉnh)
AE=ME ( 2 canh tuong ung cua tam giac BEA =tam giác BEM )
Do đo: tam giác ADE =tam giác MCE(g-c-g)
=>AD=MC ( 2canh tương ứng) (2)
Ta có : BD = BA + AD ( A nam giua B va D)
} (3)
: BC = BM + MC ( M nằm giữa B và C)
Từ (1) , (2) va (3) suy ra BD =BC
___c) Kẻ tia BE cắt đoạn thẳng DC tại H
Ta có : BD=BC (chứng minh trên)
=> tam giác BDC là tam giác cân tại B
=>gocBDC =gocBCD ( Vi tam giác cân có 2 góc ở đáy = nhau ) .