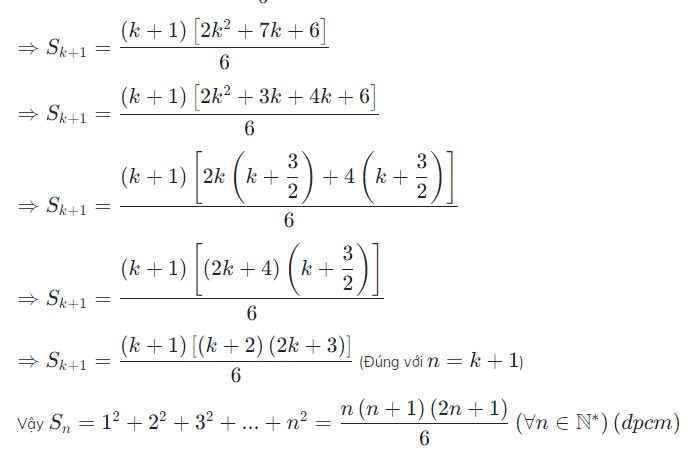chứng minh rằng với mọi số tự nhiên x và y ,ta luôn luôn có;
2x+4y +1 ko chia hết cho 2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NM
0
Những câu hỏi liên quan
LM
3
13 tháng 10 2015
Ta có :
2x + 6y = 2x + 2.3y = 2.(x + 3y) chia hết cho 2 với mọi số tự nhiên x và y
DV
13 tháng 10 2015
Ta có:
2x + 6y = 2.3y.(x + 3y) chia hết cho mọi số tự nhiên x và y
DT
1
20 tháng 10 2015
a) a,2x+6y chia hết cho 2
= 2(x+3y ) chia hết cho 2 vì 2 chia hết cho 2 nên 2 nhân với sô nào cũng chia hết cho 2
b,5x+10y chia hết cho 5
= 5(x+2y) chia hết cho 5 vì 5 chia hết cho 5 nên 5 nhân với sô nào cũng chia hết cho 5
PT
1
CM
13 tháng 4 2018
* Với n = 2 ta có 2 2 + 1 > 2.2 + 3 ⇔ 8 > 7 (đúng).
Vậy (*) đúng với n= 2 .
* Giả sử với n = k , k ≥ 2 thì (*) đúng, có nghĩa ta có: 2 k + 1 > 2 k + 3 (1).
* Ta phải chứng minh (*) đúng với n = k + 1, có nghĩa ta phải chứng minh:
2 k + 2 > 2 ( k + 1 ) + 3
Thật vậy, nhân hai vế của (1) với 2 ta được:
2.2 k + 1 > 2 2 k + 3 ⇔ 2 k + 2 > 4 k + 6 > 2 k + 5 .
( vì 4k + 6 > 4k + 5 > 2k + 5 )
Hay 2 k + 2 > 2 ( k + 1 ) + 3
Vậy (*) đúng với n = k + 1 .
Do đó theo nguyên lí quy nạp, (*) đúng với mọi số nguyên dương ≥ 2
LP
13 tháng 10 2015
a)Vì 2 chia hết cho 2 nên 2x chia hết cho 2, 6 chia hết cho 2 nên 6y chia hết cho 2. 2 số chia hết cho 2 có tổng chia hết cho 2 nên x và y nhân với 2 và 6 thì luôn chia hết cho 2
b)Vì 3 chia hết cho 3 nên 3x chia hết cho 3, 12 chia hết cho 3 nên 12y chia hết cho 3. 2 số chia hết cho 3 có tổng chia hết cho 3 nên x và y nhân với 3 và 12 thì luôn chia hết cho 3
c)Vì 5 chia hết cho 5 nên 5x chia hết cho 5, 10 chia hết cho 5 nên 10y chia hết cho 5. 2 số chia hết cho 5 có tổng chia hết cho 5 nên x và y nhân với 5 và 10 thì luôn chia hết cho 5
d) Vì 9 chia hết cho 9 nên 9x chia hết cho 9, 27 chia hết cho 9 nên 27y chia hết cho 9. 2 số chia hết cho 9 có tổng chia hết cho 9 nên x và y nhân với 9 và 27 thì luôn chia hết cho 9
ND
Nguyễn Đức Trí
VIP
4 tháng 10 2023
\(A=405^n+2^{405}+17^{37}\left(n\in N\right)\)
\(\Rightarrow A=\overline{.....5}+2^{4.101}.2+17^{4.9}.17\)
\(\Rightarrow A=\overline{.....5}+\overline{.....6}.2+\overline{.....1}.17\)
\(\Rightarrow A=\overline{.....5}+\overline{.....2}+\overline{.....7}\)
\(\Rightarrow A=\overline{......4}\)
Vì chữ số tận cùng của \(A\) là \(4\)
Nên \(A=405^n+2^{405}+17^{37}\) không chia hết cho \(10\)
\(\Rightarrow dpcm\)
NN
2
18 tháng 5 2022
\(\left(x+y\right)^2\ge4xy\)
\(\Leftrightarrow x^2+2xy+y^2\ge4xy\)
\(\Leftrightarrow x^2-2xy+y^2\ge0\)
\(\Leftrightarrow\left(x-y\right)^2\ge0\) (luôn đúng với \(\forall x,y\))
-Vậy BĐT đã được c/m.
-Dấu "=" xảy ra khi \(x=y\)
4 tháng 10 2023
Bước 1: Chứng minh công thức đúng cho n = 1. Khi n = 1, ta có: 1² = 1 = 1 . (1 + 1) . (2 . 1 + 1) / 6 = 1. Vậy công thức đúng cho n = 1.
Bước 2: Giả sử công thức đúng cho n = k, tức là 1² + 2² + ... + k² = k . (k + 1) . (2k + 1) / 6. Ta cần chứng minh công thức đúng cho n = k + 1, tức là 1² + 2² + ... + k² + (k + 1)² = (k + 1) . (k + 1 + 1) . (2(k + 1) + 1) / 6.
Bước 3: Chứng minh công thức đúng cho n = k + 1. Ta có: 1² + 2² + ... + k² + (k + 1)² = (k . (k + 1) . (2k + 1) / 6) + (k + 1)² = (k . (k + 1) . (2k + 1) + 6(k + 1)²) / 6 = (k . (k + 1) . (2k + 1) + 6(k + 1) . (k + 1)) / 6 = (k + 1) . ((k . (2k + 1) + 6(k + 1)) / 6) = (k + 1) . ((2k² + k + 6k + 6) / 6) = (k + 1) . ((2k² + 7k + 6) / 6) = (k + 1) . ((k + 2) . (2k + 3) / 6) = (k + 1) . ((k + 1 + 1) . (2(k + 1) + 1) / 6).
Vậy, công thức đã được chứng minh đúng cho mọi số tự nhiên n khác 0.
NN
1