Trong mặt phẳng tọa độ Oxy, cho đường thẳng \(d:x-y+1=0\) . Viết phương trình đường thẳng d' là ảnh của đường thẳng d qua phép đối xứng tâm \(A\left(5;-2\right)\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


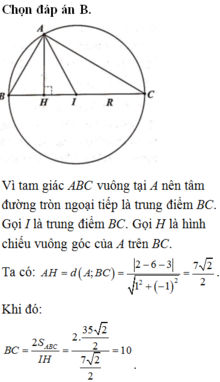
Đáp án là B

x − 3 8 − 3 = y + 6 − 11 + 6 < = > − 5 x − 5 y − 15 = 0 < = > x + y + 3 = 0

Đáp án B.
Dễ thấy d ⊥ α và − 1 ; − 2 ; − 3 ∈ α ⇒ d ⊂ α .
Ta có B = Δ ∩ Oxy ⇒ B a ; b ; 0 mà B ∈ Δ ⊂ α ⇒ 2 a + b − 2 = 0 (1).
Lại có d / / Δ ⇒ d d ; Δ = d B ; d = 3.
Đường thẳng d đi qua M 0 ; 0 ; − 1 , có u d → = 1 ; 2 ; 2 .
Do đó:
d B ; d = B M → ; u d → u d → = 2 b − 2 2 + 1 − 2 a 2 + 2 a − b 2 3 = 3 2
Từ (1), (2) suy ra:
a ; b = − 1 ; 4 → B − 1 ; 4 ; 0 a ; b = 2 ; − 2 → B 2 ; − 2 ; 0 .
Vậy A B = 7 2 .

Chọn C
Gọi giao điểm của Δ và d là B nên ta có: B (3+t;3+3t;2t) ![]()
Vì đường thẳng Δ song song với mặt phẳng (α) nên:
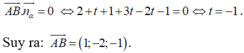
Phương trình đường thẳng Δ đi qua A và nhận 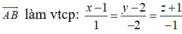

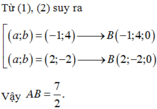


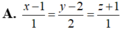

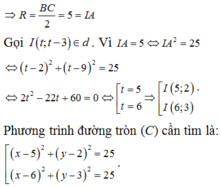

Gọi \(M\left(x;y\right)\) là điểm bất kì trên d \(\Rightarrow x-y+1=0\) (1)
Gọi \(M'\left(x';y'\right)\) là ảnh của M qua phép đối xứng tâm A \(\Rightarrow M'\in d'\)
Ta có:
\(\left\{{}\begin{matrix}x'=2.5-x\\y'=2.\left(-2\right)-y\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=10-x'\\y=-4-y'\end{matrix}\right.\)
Thế vào (1):
\(10-x'-\left(-4-y'\right)+1=0\)
\(\Leftrightarrow x'-y'-15=0\)
Vậy pt d' có dạng: \(x-y-15=0\)