Question

[Ngọc Diệu]

\(\Delta ABC\) có G trọng tâm , I là trung điểm AG, K\(\varepsilon\)AB , AK=\(\frac{1}{5}\)AB.

a.Phân tích \(\overrightarrow{AI},\overrightarrow{AK},\overrightarrow{CI},\overrightarrow{CK}\) THEO \(\overrightarrow{a}=\overrightarrow{CA},\overrightarrow{b}=\overrightarrow{CB}\)

b.CMR: C,I ,K thẳng hàng

Answer 1

[Akai Haruma]

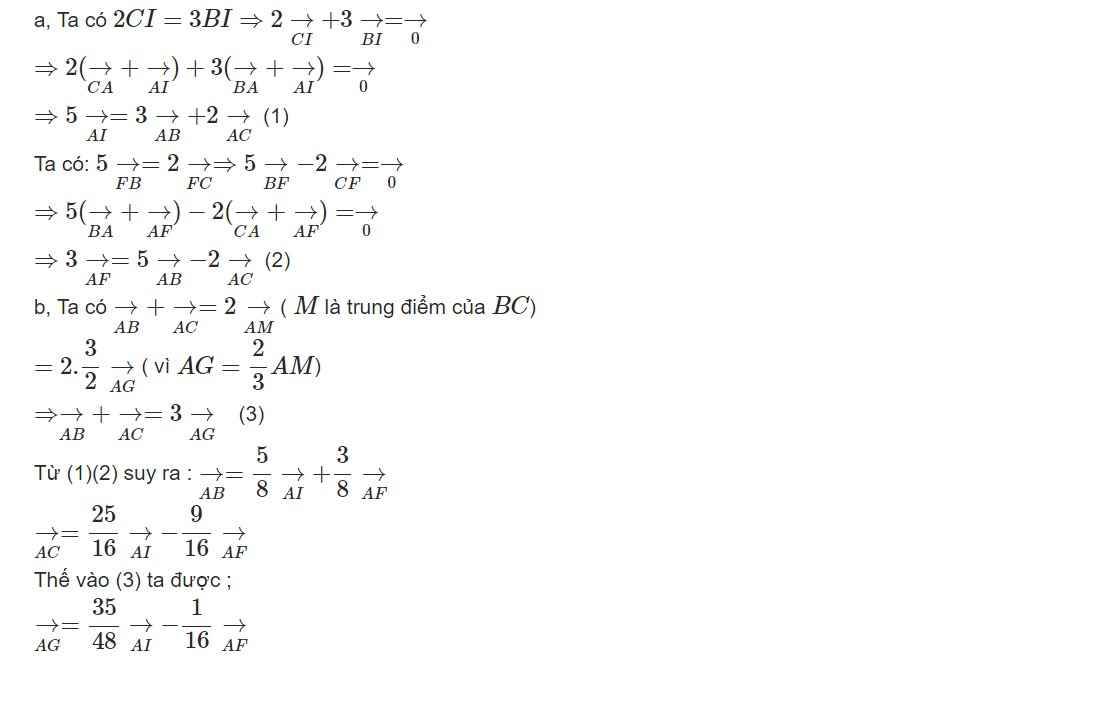
Lời giải:

a) Kéo dài $AG$ cắt $BC$ tại trung điểm $M$. Hiển nhiên $\overrightarrow{BM}, \overrightarrow{CM}$ là vecto đối nên tổng bằng vecto không.

Theo tính chất trọng tâm ta có:

$\overrightarrow{AI}=\frac{1}{2}\overrightarrow{AG}=\frac{1}{2}.\frac{2}{3}\overrightarrow{AM}=\frac{1}{3}\overrightarrow{AM}$

$=\frac{1}{6}(\overrightarrow{AM}+\overrightarrow{AM})=\frac{1}{6}(\overrightarrow{AB}+\overrightarrow{BM}+\overrightarrow{AC}+\overrightarrow{CM})$

$=\frac{1}{6}(\overrightarrow{AB}+\overrightarrow{AC})$

$=\frac{1}{6}(\overrightarrow{AC}+\overrightarrow{CB}+\overrightarrow{AC})$

$=\frac{1}{6}(2\overrightarrow{AC}+\overrightarrow{CB})$

$=\frac{-1}{3}\overrightarrow{CA}+\frac{1}{6}\overrightarrow{CB}$

$=\frac{-1}{3}\overrightarrow{a}+\frac{1}{6}\overrightarrow{b}$

----------------------

$\overrightarrow{AK}=\frac{1}{5}\overrightarrow{AB}=\frac{1}{5}(\overrightarrow{AC}+\overrightarrow{CB})=\frac{1}{5}(-\overrightarrow{CA}+\overrightarrow{CB})$

$=\frac{-1}{5}\overrightarrow{a}+\frac{1}{5}\overrightarrow{b}$

------------------

$\overrightarrow{CI}=\overrightarrow{CA}+\overrightarrow{AI}=\overrightarrow{a}-\frac{1}{3}\overrightarrow{a}+\frac{1}{6}\overrightarrow{b}$

$=\frac{2}{3}\overrightarrow{a}+\frac{1}{6}\overrightarrow{b}$

-------------------

$\overrightarrow{CK}=\overrightarrow{CA}+\overrightarrow{AK}=\overrightarrow{a}-\frac{1}{5}\overrightarrow{a}+\frac{1}{5}\overrightarrow{b}=\frac{4}{5}\overrightarrow{a}+\frac{1}{5}\overrightarrow{b}$

b)

Từ phần a ta thấy: $\overrightarrow{CI}=\frac{5}{6}\overrightarrrow{CK}$ nên $C,I,K$ thẳng hàng.

Answer 2

[Akai Haruma]

Hình vẽ: