Giải phương trình nghiệm nguyên: 9x2 + 3y2 + 6xy - 6x +2y -35 =0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Điều kiện x ≥ − 7 y ≥ − 1 3 *
x 2 + 2 x y + 8 x = 3 y 2 + 12 y + 9 ( 1 ) x 2 + 4 y + 18 − 6 x + 7 − 2 x 3 y + 1 = 0 ( 2 )
Có 1 ⇔ x 2 + 2 y + 4 x − 3 y 2 − 12 y − 9 = 0 , ta coi (1) là phương trình bậc hai ẩn x và y là tham số, giải x theo y ta được x = − 3 y − 9 x = y + 1
Với x = − 3 y − 9 thì (*) ⇒ − 3 y − 9 ≥ − 7 y ≥ − 1 3 ⇔ y ≤ − 2 3 y ≥ − 1 3 (vô lí)
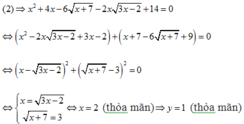
Hệ phương trình có nghiệm là 2 ; 1 ⇒ a = 2 , b = 1 ⇒ T = 24
Đáp án cần chọn là: A

\(2x^2+5xy+3y^2\\= 2x^2+2xy+3xy+3y^2\\= 2x\left(x+y\right)+3y\left(x+y\right)\\=\left(2x+3y\right)\left(x+y\right) \)
2x^2-5xy-3y^2
= 2^x + xy - 6xy - 3y^2
= x(2x + y) - 3y(2x + y)
= (2x + y)(x - 3y)

\(5x^2+2\left(3y+1\right)x+2y^2+2y-73=0\) (1)
\(\Delta'=\left(3y+1\right)^2-5\left(2y^2+2y-73\right)=-y^2-4y+366\)
\(\Delta'\) là số chính phương \(\Rightarrow-y^2-4y+366=k^2\)
\(\Leftrightarrow\left(y+2\right)^2+k^2=370=3^2+19^2=9^2+17^2\)
\(\Rightarrow\left[{}\begin{matrix}y+2=3\\y+2=19\\y+2=9\\y+2=17\end{matrix}\right.\) thế vào (1) tìm x nguyên dương

a/ \(x^2-2.4x+16+y^2+2y+1+z^2=16\Leftrightarrow\left(x-4\right)^2+\left(y+1\right)^2+z^2=16\)
\(\Rightarrow\left\{{}\begin{matrix}I\left(4;-1;0\right)\\R=\sqrt{16}=4\end{matrix}\right.\)
b/ \(x^2+y^2+z^2+2x-y+5z-\dfrac{2}{3}=0\Leftrightarrow x^2+2x+1+y^2-2.\dfrac{1}{2}y+\dfrac{1}{4}+z^2+2.\dfrac{5}{2}z+\dfrac{25}{4}=\dfrac{2}{3}+1+\dfrac{1}{4}+\dfrac{25}{4}\)
\(\Leftrightarrow\left(x+1\right)^2+\left(y-\dfrac{1}{2}\right)^2+\left(z+\dfrac{5}{2}\right)^2=\dfrac{49}{6}\) \(\Rightarrow\left\{{}\begin{matrix}I\left(-1;\dfrac{1}{2};-\dfrac{5}{2}\right)\\R=\dfrac{7}{\sqrt{6}}\end{matrix}\right.\)
P/s: câu c bạn tự làm nốt ạ!



Ta có : \(4x-5y-6xy-7=0\)
\(\Leftrightarrow12x-15y-18xy-21=0\)
\(\Leftrightarrow\left(12x-18xy\right)-15y-21=0\)
\(\Leftrightarrow6x.\left(2-3y\right)+5.\left(2-3y\right)-31=0\)
\(\Leftrightarrow\left(2-3y\right)\left(6x+5\right)=31\)
Do \(x,y\inℤ\Rightarrow\hept{\begin{cases}2-3y\inℤ\\6x+5\inℤ\end{cases}}\)
Nên \(2-3y,6x+5\) là cặp ước của \(31\).
Ta có bảng sau :
| \(2-3y\) | \(-1\) | \(1\) | \(-31\) | \(31\) |
| \(y\) | \(1\) | \(\frac{1}{3}\) | \(11\) | \(-\frac{29}{3}\) |
| \(6x+5\) | \(-31\) | \(31\) | \(-1\) | \(1\) |
| \(x\) | \(-6\) | \(\frac{13}{3}\) | \(-1\) | \(-\frac{2}{3}\) |
| Đánh giá | Chọn | Loại | Chọn | Loại |
Vậy \(\left(x,y\right)\in\left\{\left(-6,1\right);\left(-1,11\right)\right\}\) thỏa mãn đề.

`9x2 + 3y2 + 6xy - 6x + 2y - 35 = 0`
`<=> (9x2 + 6xy + y2) - 2(3x + y) + 1 + 2(y2 + 2y + 1) - 37 = 0`
`<=> (3x + y - 1)2 = 37 - 2(y + 1)^2`
Vì `(3x+y=1)^2>=0`
`=>2(y+1)^2<=37`
`=>(y+1)^2<=37/2`
Mà `(y+1)^2` là scp
`=>(y+1)^2 in {0,1,4,8,16}`
`=> y + 1 ∈{0; 1; -1; 2; -2; 3; -3; 4; -4}`
`=>y in {-1,0,-2,1,-3,2,-4,3,-5}`
Đến đây dễ rồi thay y vào rồi tìm x thôi!
\(9x^2+3y^2+6xy-6x+2y-35=0\)
\(\Leftrightarrow\left(9x^2+6xy+y^2\right)-2\left(3x+y\right)+1+2y^2+4y+2=38\)
\(\Leftrightarrow\left(3x+y-1\right)^2+2\left(y+1\right)^2=38\)(*)
\(\Rightarrow\left(3x+y-1\right)^2=38-2\left(y+1\right)^2\le38\)
\(\Rightarrow-\sqrt{38}\le3x+y-1\le\sqrt{38}\)
Từ (*) suy ra 3x + y - 1 chẵn mà 3x + y - 1 nguyên nên \(3x+y-1\in\left\{\pm6;\pm4;\pm2;0\right\}\)
* Nếu \(3x+y-1=\pm6\)thì \(2\left(y+1\right)^2=2\Rightarrow y+1=\pm1\Rightarrow\orbr{\begin{cases}y=-2\\y=0\end{cases}}\)
Th1: \(3x+y-1=6\)
+) \(y=-2\Rightarrow x=3\)
+) \(y=0\Rightarrow x=\frac{7}{3}\left(L\right)\)
Th2: \(3x+y-1=-6\)
+) \(y=-2\Rightarrow x=-1\)
+) \(y=0\Rightarrow x=\frac{-5}{3}\left(L\right)\)
* Nếu \(3x+y-1=\pm4\)thì \(2\left(y+1\right)^2=22\left(L\right)\)
* Nếu \(3x+y-1=\pm2\)thì \(2\left(y+1\right)^2=34\left(L\right)\)
* Nếu 3x + y - 1 = 0 thì \(2\left(y+1\right)^2=38\left(L\right)\)
Vậy phương trình có 2 cặp nghiệm nguyên \(\left(x,y\right)\in\left\{\left(3;-2\right);\left(-1;-2\right)\right\}\)