BT1: Cho \(\Delta ABC\), có AB=6cm, AC=8cm, BC= 10cm.
a) CM: \(\Delta ABC\) là \(\Delta\)vuông.
b) Tính các góc của \(\Delta ABC\)
c) Kẻ đường cao AH\(\perp BC\). tính AH,BH,CH.
Không cần vẽ hình đâu ạ.tính câu b,c thôi ạ
Cảm ơn ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
19 tháng 3 2022
hình bạn tự vé nhé.
tam giác ABC vuông tại A nên theo định lý PY-Ta-Go ta có:
\(AB^2+AC^2=BC^2\)
\(\Rightarrow6^2+8^2=BC^2\)
\(\Rightarrow BC=10\left(DO-BC>0\right)\)
b) xét \(\Delta ABC\) VÀ \(\Delta HBA\) CÓ:
\(\widehat{BAC}=\widehat{AHB}\)
\(\widehat{B}\) CHUNG
\(\Rightarrow\Delta ABC\) đồng dạng vs \(\Delta HBA\)
19 tháng 3 2022
c)sửa đề:\(AB^2=BH.BC\)
TA CÓ: \(\Delta ABC\text{ᔕ}\Delta HBA\)
\(\Rightarrow\frac{AB}{BH}=\frac{BC}{AB}\left(tsđd\right)\)
\(\Rightarrow AH^2=BH.BC\)
9 tháng 10 2021
\(a,\) Vì \(10^2=6^2+8^2\Leftrightarrow BC^2=AB^2+AC^2\) nên tg ABC vg tại A (PTG đảo)
\(b,\) Áp dụng HTL:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\\AH^2=BH\cdot HC\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}BH=\dfrac{AB^2}{BC}=3,6\left(cm\right)\\CH=\dfrac{AC^2}{BC}=6,4\left(cm\right)\\AH=\sqrt{3,6\cdot6,4}=4,8\left(cm\right)\end{matrix}\right.\)
\(c,\dfrac{AD}{DC}=\dfrac{AB}{BC}=\dfrac{3}{5}\left(t/c.đường.p/g\right)\\ \Rightarrow AD=\dfrac{3}{5}DC\)
Mà \(AD+DC=AC=8\)
\(\Rightarrow\dfrac{8}{5}DC=8\Rightarrow DC=5\left(cm\right)\\ \Rightarrow AD=3\left(cm\right)\)
\(\Rightarrow S_{ABD}=\dfrac{1}{2}AB\cdot AD=\dfrac{1}{2}\cdot6\cdot3=9\left(cm^2\right)\)
\(\Rightarrow S_{BCD}=S_{ABC}-S_{ADB}=\dfrac{1}{2}AB\cdot AC-9=24-9=15\left(cm^2\right)\)
16 tháng 4 2021
a/ Xét \(\Delta ABC\) và \(\Delta HAC\) có :
\(\left\{{}\begin{matrix}\widehat{C}chung\\\widehat{BAC}=\widehat{AHC}=90^0\end{matrix}\right.\)
\(\Leftrightarrow\Delta ABC\sim HAC\left(g-g\right)\)
b/ \(BC=\sqrt{AB^2+AC^2}=10cm\)
\(AH.BC=AB.AC\Leftrightarrow AH=\dfrac{AB.AC}{BC}=4,8cm\)
c/ \(\Delta HEA\sim\Delta CEH\left(g-g\right)\)
\(\Leftrightarrow\dfrac{HE}{CE}=\dfrac{EA}{HE}\Leftrightarrow HE^2=EA.EC\left(đpcm\right)\)
16 tháng 4 2021
a) Xét ΔHAC và ΔABC có:
∠(ACH ) là góc chung
∠(BAC)= ∠(AHC) = 90o
⇒ ΔHAC ∼ ΔABC (g.g)
b) Xét ΔHAD và ΔBAH có:
∠(DAH ) là góc chung
∠(ADH) = ∠(AHB) = 90o
⇒ ΔHAD ∼ ΔBAH (g.g)
c) Tứ giác ADHE có 3 góc vuông ⇒ ADHE là hình chữ nhật.
⇒ ΔADH= ΔAEH ( c.c.c) ⇒ ∠(DHA)= ∠(DEA)
Mặt khác: ΔHAD ∼ ΔBAH ⇒ ∠(DHA)= ∠(BAH)
∠(DEA)= ∠(BAH)
Xét ΔEAD và ΔBAC có:
∠(DEA)= ∠(BAH)
∠(DAE ) là góc chung
ΔEAD ∼ ΔBAC (g.g)
d) ΔEAD ∼ ΔBAC
ΔABC vuông tại A, theo định lí Pytago:
Theo b, ta có:
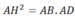
SINB=AC/BC=8/10=4/5
=> GÓC B = XẤP XỈ 53'.
=> GÓC C=37'.
C)CÓ AB.AC=AH.BC
<=> 6.8=AH.10
<=>AH=6.8/10=4,8 .
LẠI CÓ BC.HB=AB2
<=> HB=AB2/BC
<=>HB=36/10=3,6.
=>HC=BC-HB=10-3,6=6,4.