Nghiệm của phương trình : \(sinx-\sqrt{3}.cosx=2sin3x\) là ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
30 tháng 7 2021
\(\Leftrightarrow\dfrac{1}{2}sinx+\dfrac{\sqrt{3}}{2}cosx=sin3x\)
\(\Leftrightarrow sin\left(x+\dfrac{\pi}{3}\right)=sin3x\)
\(\Leftrightarrow\left[{}\begin{matrix}3x=x+\dfrac{\pi}{3}+k2\pi\\3x=\dfrac{2\pi}{3}-x+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{6}+k\pi\\x=\dfrac{\pi}{6}+\dfrac{k\pi}{2}\end{matrix}\right.\)
\(\Leftrightarrow x=\dfrac{\pi}{6}+\dfrac{k\pi}{2}\)
AA
2
24 tháng 8 2021
2sin3x = cosx (sin2x + cos2x)
⇔ 2sin3x - sin2x cosx - cos3x = 0
+ Xét cosx = 0 ........
+ Xét cosx khác 0 rồi chia cho cos3x rồi đưa về phương trình bậc 3 của tanx
24 tháng 8 2021
sin3x + cos3x = sinx - cosx
Nhân cos2x + sin2x là thành câu trên
NV
Nguyễn Việt Lâm
Giáo viên
30 tháng 7 2021
2.1
a.
\(\Leftrightarrow sinx-cosx=\dfrac{\sqrt{2}}{2}\)
\(\Leftrightarrow\sqrt{2}sin\left(x-\dfrac{\pi}{4}\right)=\dfrac{\sqrt{2}}{2}\)
\(\Leftrightarrow sin\left(x-\dfrac{\pi}{4}\right)=\dfrac{1}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}x-\dfrac{\pi}{4}=\dfrac{\pi}{6}+k2\pi\\x-\dfrac{\pi}{4}=\dfrac{5\pi}{6}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5\pi}{12}+k2\pi\\x=\dfrac{13\pi}{12}+k2\pi\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
30 tháng 7 2021
b.
\(cosx-\sqrt{3}sinx=1\)
\(\Leftrightarrow\dfrac{1}{2}cosx-\dfrac{\sqrt{3}}{2}sinx=\dfrac{1}{2}\)
\(\Leftrightarrow cos\left(x+\dfrac{\pi}{3}\right)=\dfrac{1}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}x+\dfrac{\pi}{3}=\dfrac{\pi}{3}+k2\pi\\x+\dfrac{\pi}{3}=-\dfrac{\pi}{3}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=k2\pi\\x=-\dfrac{2\pi}{3}+k2\pi\end{matrix}\right.\)
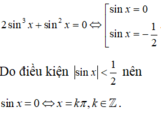
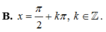
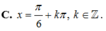
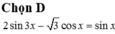
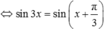
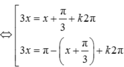
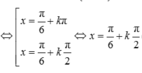
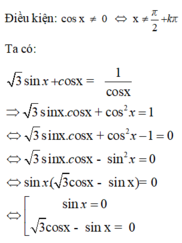
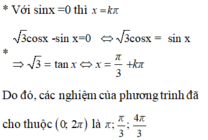
\(\frac{1}{2}sinx-\frac{\sqrt{3}}{2}cosx=sin3x\)
\(\Leftrightarrow sin3x=sin\left(x-\frac{\pi}{3}\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}3x=x-\frac{\pi}{3}+k2\pi\\3x=\frac{4\pi}{3}-x+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\frac{\pi}{6}+k\pi\\x=\frac{\pi}{3}+\frac{k\pi}{2}\end{matrix}\right.\)