Một xe chuyển động chậm dần đều: quãng đường xe đi được trong 2 giây đầu dài hơn quãng đường xe đi được trong 2 giây cuối là 36 m ( ), quãng đường giữa hai khoảng thời gian trên là 160 m ( ). Tìm thời gian chuyển động chậm dần đều cho đến khi dừng lại ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
30 tháng 7 2019
Ta có
Phương trình quãng đường chuyển động của xe:
S = v 0 t + 1 2 a t 2
Phương trình vận tốc của xe:v=v0+at
Quãng đường xe đi được trong giây đầu tiên:
s 1 = v 0 + 1 2 a
Quãng đường xe đi được đến khi dừng lại:
S = v 0 t + 1 2 a t 2
Quãng đường xe đi được trong(t−1)giây là:
s t − 1 = v 0 ( t − 1 ) + 1 2 a ( t − 1 ) 2
⇒ Quãng đường xe đi được trong giây cuối cùng là:
Δ S = S − S t − 1 = v 0 t + 1 2 a t 2 − v 0 ( t − 1 ) − 1 2 a t - 1 2
= v 0 + a t − 1 2 a
Theo đầu bài ta có: 15 Δ s = s 1
⇔ v 0 + 1 2 a = 15 ( v 0 + a t − 1 2 a )
Lại có: v 0 + a t = v d u n g = 0 m / s
⇒ v 0 + 1 2 a = − 15 a 2 ⇒ v 0 = − 8 a
Áp dụng công thức liên hệ:v2−v02=2as
⇔0−(−8a)2=2.a.96⇒a=−3m/s2
Hợp lực tác dụng vào vật có độ lớn:
F = m a = 1,2.1000.3 = 3600 ( N )
Đáp án: C
27 tháng 11 2021
Vận tốc xe đi trên quãng đường:
\(v=\dfrac{4}{2}=2\)m/s
Thời gian xe đi cả quãng đường:
\(t=\dfrac{225}{2}=112,5s\)
Quãng đường xe đi trong 110,5s:
\(S=110,5\cdot2=221m\)
Quãng đường xe đi trong 2s cuối:
\(S'=225-221=4m\)
VT
29 tháng 8 2017
Chọn C.
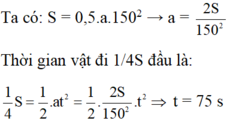
→ Thời gian vật đi 3/4 S cuối = 150 – 75 = 75 s.
15 tháng 7 2019
1)
v0=0
Sgiây thứ 3 = 5m \(\Leftrightarrow S_{giâythứ3}=v_0t+\frac{1}{2}at^2-v_0\left(t-1\right)-\frac{1}{2}a\left(t-1\right)^2=v_0+a\left(t-\frac{1}{2}\right)=0+a\left(3-\frac{1}{2}\right)=\frac{5}{2}a\)
=> \(\frac{5}{2}a=5\)
=> a =2\(m/s^2\)
Quãng đường xe đi được sau 10s là:
t =10s => \(s=v_0t+\frac{1}{2}at^2=\frac{1}{2}.2.10^2=100\left(m\right)\)
VT
14 tháng 3 2019
Chọn D.
Từ : v = v 0 + at s = v 0 t + 0 , 5 at 2 → khi dừng lại 0 = 40 + a . 8 s = 40 . 8 + 0 , 5 a . 8 2
⇒ a = - 5 ( m / s 2 ) s = 160 ( m ) .
Q
8 tháng 8 2021
a, đổi 18km/h=5m/s
ta có 5s vật đi đc \(S_5=5.5+\dfrac{1}{2}a5^2\)
4s vật đi đc \(S_4=5.4+\dfrac{1}{2}a4^2\)
ta có \(\left(\dfrac{1}{2}.a.25+25\right)-\left(\dfrac{1}{2}a.16+20\right)=5,45\Rightarrow a=0,1\left(m/s^2\right)\)
b, S sau 10s
\(S_{10}=5.10+\dfrac{1}{2}.0,1.10^2=55\left(m\right)\)
S sau 9s
\(S_9=5.9+\dfrac{1}{2}.0,1.9^2=49,05\left(m\right)\)
\(=>S=S_{10}-S_9=...\)