tìm m để pt sau có nghiệm:
a, m.cosx= m+1
b, sin6x+cos6x-cos4x-m=0
c, cos6x+sin6x=m( sin4x+ cos4x)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



(1) trở thành 4t2 – 2t -6 – m = 0 (2); △ ' = 25 + 4 m .
Để (1) vô nghiệm, ta sẽ tìm m sao cho (1) có nghiệm rồi sau đó phủ định lại.
(1) có nghiệm thì (2) phải có nghiệm thoả t o ∈ - 1 ; 1
Nếu 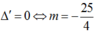 , (2) có nghiệm kép
, (2) có nghiệm kép 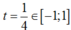 nên
nên ![]() thoả (1) có nghiệm.
thoả (1) có nghiệm.
Nếu ![]() , khi đó (2) phải có hai nghiệm phân biệt thoả
, khi đó (2) phải có hai nghiệm phân biệt thoả 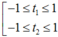
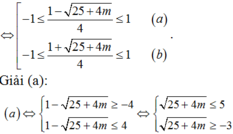
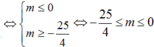
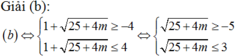
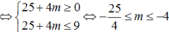


a, Ta có: sin 4 x + cos 4 x = sin 2 x + cos 2 x 2 - 2 sin 2 x . cos 2 x = 1 - 2 sin 2 x . cos 2 x
b, Ta có: sin 6 x + cos 6 x = sin 2 x + cos 2 x 3 - 3 sin 2 x cos 2 x sin 2 x + cos 2 x = 1 - 3 sin 2 x cos 2 x

Chọn A.
Ta có:
+ sin4x + cos4x = (sin2x + cos2x)2 - 2sin2x.cos2x = 1 - 2sin2x.cos2x.
+ sin4x + cos4x = 1 - 3sin2x.cos2x.
Do đó
A = 3(1 - 2sin2x.cos2x) - 2(1 - 3sin2x.cos2x) = 1.

\(P=\dfrac{-2sin5x.sinx-sinx}{2sin5x.cosx+cosx}=\dfrac{-sinx\left(2sin5x+1\right)}{cosx\left(2sin5x+1\right)}=-tanx\)

\(A=3\left[\left(sin^2x+cos^2x\right)^2-2\cdot sin^2x\cdot cos^2x\right]-2\left[\left(sin^2x+cos^2x\right)^3-3\cdot sin^2x\cdot cos^2x\left(sin^2x+cos^2x\right)\right]\)
\(=3\left[1-2\cdot sin^2x\cdot cos^2x\right]-2\left[1-3\cdot sin^2x\cdot cos^2x\right]\)
\(=3-6\cdot sin^2x\cdot cos^2x-2+6\cdot sin^2x\cdot cos^2x\)
=1

Chứng minh các biểu thức đã cho không phụ thuộc vào x.
f(x) = 1 ⇒ f′(x) = 0

\(y=\dfrac{4}{3}\left(\sin^6x+\cos^6x\right)+\cos4x-1\)
\(\sin^6x+\cos^6x=\left(\sin^2x+\cos^2x\right)\left(\sin^4x-\sin^2x\cdot\cos^2x+\cos^4x\right)\\ =\left(\sin^2x+\cos^2x\right)^2-3\sin^2x\cdot\cos^2x=1-\dfrac{3}{4}\sin^22x\)
Do \(0\le\sin^22x\le1\Leftrightarrow\dfrac{3}{4}\cdot0\ge-\dfrac{3}{4}\sin^22x\ge-\dfrac{3}{4}\)
\(\Leftrightarrow1\ge1-\dfrac{3}{4}\sin^22x\ge1-\dfrac{3}{4}=\dfrac{1}{4}\\ \Leftrightarrow\dfrac{4}{3}\ge\dfrac{4}{3}\left(\sin^6x+\cos^6x\right)\ge\dfrac{1}{4}\cdot\dfrac{4}{3}=\dfrac{1}{3}\)
Ta có \(-1\le\cos4x\le1\)
\(\Leftrightarrow\dfrac{1}{3}-1-1\le\dfrac{4}{3}\left(\sin^6x+\cos^6x\right)+\cos4x-1\le\dfrac{4}{3}+1-1\\ \Leftrightarrow-\dfrac{5}{3}\le y\le\dfrac{4}{3}\)
Vậy \(y_{min}=-\dfrac{5}{3};y_{max}=\dfrac{4}{3}\)
\(y=\dfrac{4}{3}\left(sin^6x+cos^6x\right)+cos4x-1\)
\(y=\dfrac{4}{3}\left(\dfrac{5}{8}+\dfrac{3}{8}cos4x\right)+cos4x-1\)
\(y=\dfrac{3}{2}cos4x-\dfrac{1}{6}\)
\(-1\le cos4x\le1\Rightarrow-\dfrac{5}{3}\le y\le\dfrac{4}{3}\)
\(y_{min}=-\dfrac{5}{3}\) khi \(cos4x=-1\)
\(y_{max}=\dfrac{4}{3}\) khi \(cos4x=1\)
a/ \(m=0\) pt vô nghiêm
Với \(m\ne0\Rightarrow cosx=\frac{m+1}{m}\)
\(-1\le cosx\le1\Rightarrow-1\le\frac{m+1}{m}\le1\)
\(\Rightarrow m\le-\frac{1}{2}\)
b/ \(\left(sin^2x+cos^2x\right)^3-3sin^2x.cos^2x\left(sin^2x+cos^2x\right)-cos4x=m\)
\(\Leftrightarrow1-\frac{3}{4}sin^22x-cos4x=m\)
\(\Leftrightarrow1-\frac{3}{4}sin^22x-\left(1-2sin^22x\right)=m\)
\(\Leftrightarrow\frac{5}{4}sin^22x=m\)
Do \(0\le\frac{5}{4}sin^22x\le\frac{5}{4}\Rightarrow0\le m\le\frac{5}{4}\)
c/ \(\Leftrightarrow1-\frac{3}{4}sin^22x=m\left(1-\frac{1}{4}sin^22x\right)\)
\(\Leftrightarrow\left(m-3\right)sin^22x=4m-4\)
- Với \(m=3\) pt vô nghiệm
- Với \(m\ne3\Rightarrow sin^22x=\frac{4m-4}{m-3}\)
Do \(0\le sin^22x\le1\Rightarrow0\le\frac{4m-4}{m-3}\le1\)
\(\Rightarrow\frac{1}{3}\le m\le1\)