Gọi S là tập hợp tất cả các gtri thực của m sao cho f(x)=|x3- 3x+m|≤16,∀∈[0;3]. Tổng tất cả phần tử S bằng bao nhiêu?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
12 tháng 12 2018
Đáp án B.
Xét f x = x 3 − 3 x + m trên đoạn 0 ; 2
Ta có: f ' x = 3 x 3 3 = 0 ⇒ x = 1
Lại có:
f 0 = m ; f 1 = m − 2 ; f 2 = m + 2
Do đó: f x ∈ m − 2 ; m + 2
Nếu
m − 2 ≥ 0 ⇒ Max 0 ; 2 f x = m + 2 = 3 ⇔ m = 1 (loại).
Nếu m − 2 < 0 ⇒ Max 0 ; 2 f x = m + 2 Max 0 ; 2 f x = 2 − m
TH1: Max 0 ; 2 f x = m + 2 = 3 ⇔ m = 1 ⇒ 2 − m = 1 < 3 t / m
TH2: Max 0 ; 2 f x = 2 − m = 3 ⇔ m = − 1 ⇒ m + 2 = 1 < 3 t / m
Vậy m = 1 ; m = − 1 là giá trị cần tìm.
CM
22 tháng 9 2018
HD: Hoành độ giao điểm của (C) và d là nghiệm phương trình:
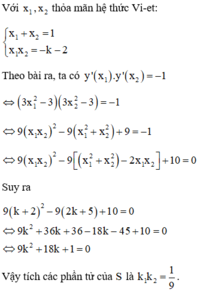
Chọn
CM
15 tháng 12 2019
+ Xét hàm số f(x) = x3-3x+ m là hàm số liên tục trên đoạn [0; 2] .
Ta có đạo hàm f’ (x) = 3x2- 3 và f’ (x) = 0 khi x= 1 ( nhận ) hoặc x= -1( loại)
+ Suy ra GTLN và GTNN của f(x) thuộc { f(0); f(1) ; f(2) }={m;m-2; m+2}.
+ Xét hàm số y = x 3 - 3 x + m trên đoạn [0; 2 ] ta được giá trị lớn nhất của y là
m a x m ; m - 2 ; m + 1 = 3 .
TH1: m= 3 thì max {1;3;5}= 5 ( loại )
TH2: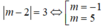 
+ Với m= -1. Ta có max {1; 3}= 3 (nhận).
+Với m= 5. Ta có max { 3;5;7}= 7 (loại).
TH3: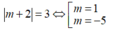 
+ Với m= 1. Ta có max {1; 3}= 3 (nhận).
+ Với m= -5. Ta có max {3;5;7}= 7 (loại).
Do đó m= -1 hoặc m= 1
Vậy tập hợp S có phần tử.
Chọn B.
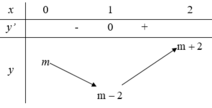
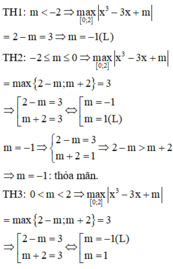
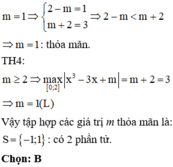
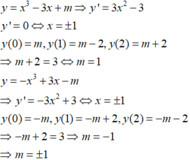
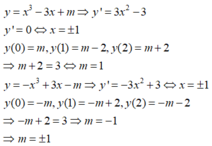
\(\Leftrightarrow\max\limits_{\left[0;3\right]}f\left(x\right)\le16\)
Trên \(\left[0;3\right]\) xét hàm \(g\left(x\right)=x^3-3x+m\Rightarrow g'\left(x\right)=3x^2-3=0\Rightarrow x=1\)
Ta có: \(g\left(0\right)=m;\) \(g\left(1\right)=m-2\) ; \(g\left(3\right)=m+21\)
\(\Rightarrow\max\limits_{\left[0;3\right]}f\left(x\right)=max\left\{\left|m-2\right|;\left|m+18\right|\right\}\)
TH1: \(\left\{{}\begin{matrix}\left|m-2\right|\ge\left|m+18\right|\\\left|m-2\right|\le16\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m\le-8\\-14\le m\le18\end{matrix}\right.\)
\(\Rightarrow-14\le m\le-8\)
TH2: \(\left\{{}\begin{matrix}\left|m+18\right|\ge\left|m-2\right|\\\left|m+18\right|\le16\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m\ge-8\\-34\le m\le-2\end{matrix}\right.\)
\(\Rightarrow-8\le m\le-2\)
Vậy \(-14\le m\le-2\)