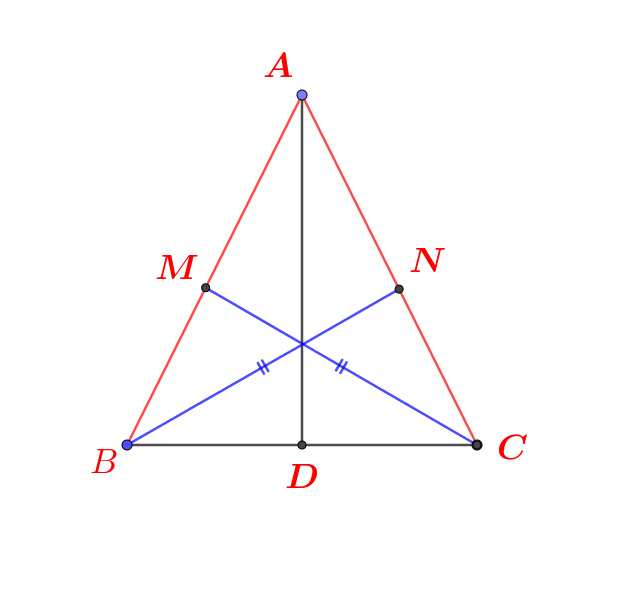
Cho tam giác ABC ,có đường phân giác AD(D thuộc BC).M,N lần lượt thuộc AB,AC sao cho BD=BM,CD=CN.Biết BN=CM.Chứng minh AB=AC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
6 tháng 10 2019
Xét \(\Delta ABC\) ta có :
AD là tia phân giác của \(\widehat{BAC}\)
\(\Leftrightarrow\frac{AB}{AC}=\frac{BD}{DC}\) ( tính chất đường phân giác trong tam giác )
\(\Leftrightarrow\frac{AB}{AC}=\frac{MB}{NC}\)
\(\Leftrightarrow\frac{AB}{MB}=\frac{AC}{NC}\)
Xét \(\Delta ABC\) có : \(\frac{AB}{MB}=\frac{AC}{NC}\)
\(\Leftrightarrow MN//BC\) ( điịnh lí Ta - lét đảo )
Chúc bạn học tốt !!!
10 tháng 3 2023
a: \(CB=\sqrt{12^2+16^2}=20\left(cm\right)\)
AH=12*16/20=9,6cm
Xet ΔABC có AD là phân giác
nên BD/AB=CD/AC
=>BD/3=CD/4=(BD+CD)/(3+4)=20/7
=>BD=60/7cm; CD=80/7cm
b: Sửa đề: AB,AC
Xét tứ giác AMHN có
góc AMH=góc ANH=góc MAN=90 độ
=>AMHN là hình chữ nhật
AM=AH^2/AB=9,6^2/12=7,68(cm)
AN=AH^2/AC=9,6^2/16=5,76(cm)
\(S_{AMHN}=7.68\cdot5.76=44.2368\left(cm^2\right)\)
7 tháng 1 2023
a: Xét ΔABD và ΔAMD có
AB=AM
góc BAD=góc MAD
AD chung
Do đó; ΔABD=ΔAMD
b: Xét ΔDBN và ΔDMC có
góc DBN=góc DMC
DB=DM
góc BDN=góc MDC
Do đó; ΔDBN=ΔDMC
=>BN=MC
c: Xét ΔANC có AB/BN=AM/MC
nên BM//CN
26 tháng 7 2023
MN//BC
=>BM/BA=CN/CA
=>BD/BA=CN/CA
mà BD/BA=CD/CA
nên CD/CA=CN/CA
=>CD=CN
=>ΔCDN cân tại C
=>góc CDN=góc CND
=>góc MND=góc CND
=>ND là phân giác của góc MNC