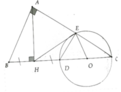
cho tam giác ABC vuông tại A . AH là đường cao , AB=8cm , BC = 16cm.Gọi D là điểm đối xứng với B qua H. Vẽ đường tròn đường kính CD cắt AC ở E . chứng minh:
a, HE là tiếp tuyến của đường tròn đường kính CD
b, Tính độ dài đường thẳng HE.
Câc bạn giải giúp mình nhé, mình đang cần gấp . Cảm ơn!



a) E nằm trên đường tròn đường kính CD
=> Tam giác CDE vuông tại E
=> DE // AB
Gọi M là trung điểm của AE
HM là đường trung bình của hình thang ABDE
=> HM // AB => \(HM\perp AB\)
=> Tam giác AHE cân tại H => \(\widehat{AEH}=\widehat{EAH}\)
Tam giác COE cân tại O => \(\widehat{OEC}=\widehat{OCE}\)
=> \(\widehat{OEC}+\widehat{AEH}=\widehat{OCE}+\widehat{EAH}=90^o\)
=> \(HE\perp OE\)=> Đpcm
b) Tam giác ABC vuông tại A
=> \(BC^2=AB^2+AC^2=289\)
=> BC = 17
Tam giác ABC vuông tại A, đường cao AH
=> AB . AC = AH . BC
=> \(HE=AH=\frac{120}{17}\)