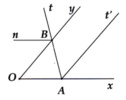
cho xOy = 40 độ . Lấy điểm A t nằm trên cùng nửa mặt phẳng có bờ là đường thẳng Ox chứa tia Oy sao cho At cắt tia Oy tại B và OAt = 100 độ . Gọi Am là tia phân giác của góc xAt.
a) Chứng minh rằng AM // Oy
b) Trên nửa mặt phẳng không chứa điểm A bờ là đường thẳng chứa tia Oy, vẽ tia Bn. Hỏi để Bn // Ox thì số đo góc OBn phải bằng bao nhiêu

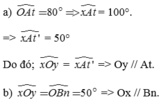
Bài giải
a.
\(\widehat{OAt }+\widehat{ tAx }=180^o\) (2 góc kề bù)
\(100^o+\widehat{tAx}=180^o\)
\(\widehat{tAx}=80^o\)
Am là tia phân giác của \(\widehat{tAx}\)
=> \(\widehat{tAm}\) = \(\widehat{mAx}\) = \(\frac{\widehat{tAx}}{2}=\frac{80^o}{2}=40^o\)
mà \(\widehat{xOy}=40^o\)
=> \(\widehat{xOy}=\widehat{xAm}\)
mà 2 góc này ở vị trí đồng vị
=> Oy // Am
b.
Bn // Ox
<=> \(\widehat{nBO}=\widehat{xOB}\) (2 góc so le trong)
mà \(\widehat{xOB}=40^o\)
=>\(\widehat{nBO}=40^o\)