Tổng 2 nghiệm âm liên tiếp lớn nhất của pt: \(4\sin^3x-\sin X+-\cos X=0\) bằng bn? (Bỏ dấu cộng. Nhầm ạ)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
9 tháng 8 2020
1.
\(cos^2x-sin^2x=cosx\Leftrightarrow cos2x=cosx\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=x+k2\pi\\2x=-x+k2\pi\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=k2\pi\\x=\frac{k2\pi}{3}\end{matrix}\right.\)
Nghiệm âm lớn nhất là \(x=-\frac{2\pi}{3}\)
2.
ĐKXĐ: ...
\(\Leftrightarrow1+sinx+cosx+\frac{sinx}{cosx}=0\)
\(\Leftrightarrow1+cosx+sinx\left(\frac{cosx+1}{cosx}\right)=0\)
\(\Leftrightarrow\left(1+cosx\right)\left(1+\frac{sinx}{cosx}\right)=0\)
\(\Leftrightarrow\left(1+cosx\right)\left(1+tanx\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=-1\\tanx=-1\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=\pi+k2\pi\\x=-\frac{\pi}{4}+k\pi\end{matrix}\right.\)
Nghiệm dương bé nhất là \(x=\frac{3\pi}{4}\)
KB
16 tháng 7 2021
\(\sqrt{3}cosx+2sin^2\left(\dfrac{x}{2}-\pi\right)=1\)
\(\Leftrightarrow\sqrt{3}cosx+2sin^2\dfrac{x}{2}=1\)
\(\Leftrightarrow\sqrt{3}cosx-cosx=0\Leftrightarrow cosx=0\Leftrightarrow x=\dfrac{\pi}{2}+k\pi\) ( k thuộc Z )
Vậy ...
NV
Nguyễn Việt Lâm
Giáo viên
16 tháng 7 2021
22.
Nhận thấy \(cosx=0\) không phải nghiệm, chia 2 vế cho \(cos^2x\)
\(3tan^2x+2tanx-1=0\)
\(\Leftrightarrow\left[{}\begin{matrix}tanx=-1\\tanx=\dfrac{1}{3}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{\pi}{4}+k\pi\\x=arctan\left(\dfrac{1}{3}\right)+k\pi\end{matrix}\right.\)
Nghiệm dương nhỏ nhất của pt là: \(x=arctan\left(\dfrac{1}{3}\right)\)
NV
Nguyễn Việt Lâm
Giáo viên
1 tháng 8 2020
Số âm càng lớn thì trị tuyệt đối càng nhỏ, do đó ta chỉ cần tìm k lớn nhất sao cho nghiệm x âm
Để khỏi nhầm lẫn thì 2 tham số 1 cái đặt là k 1 cái đặt là n đi
Tìm nghiệm âm: \(\left[{}\begin{matrix}\frac{7\pi}{36}+\frac{k2\pi}{3}< 0\\\frac{11\pi}{36}+\frac{n2\pi}{3}< 0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}k< -\frac{7}{24}\\n< -\frac{11}{24}\end{matrix}\right.\) mà k; n nguyên \(\Rightarrow k=n=-1\)
Thay vào nghiệm của pt: \(\left[{}\begin{matrix}x=\frac{7\pi}{36}-\frac{2\pi}{3}=-\frac{17\pi}{36}\\x=\frac{11\pi}{36}-\frac{2\pi}{3}=-\frac{13\pi}{36}\end{matrix}\right.\)
So sánh 2 nghiệm này ta thấy \(-\frac{13\pi}{36}>-\frac{17\pi}{36}\) nên \(x=-\frac{13\pi}{36}\) là nghiệm âm lớn nhất của pt
NV
Nguyễn Việt Lâm
Giáo viên
31 tháng 7 2020
21.
\(\Leftrightarrow\left[{}\begin{matrix}sinx+1=0\\sinx-\sqrt{2}=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}sinx=-1\\sinx=\sqrt{2}>1\left(vn\right)\end{matrix}\right.\)
\(\Rightarrow x=-\frac{\pi}{2}+k2\pi\)
\(x\in\left[-2017;2017\right]\Rightarrow-2017\le-\frac{\pi}{2}+k2\pi\le2017\)
\(\Rightarrow\frac{\frac{\pi}{2}-2017}{2\pi}\le k\le\frac{\frac{\pi}{2}+2017}{2\pi}\)
\(\Rightarrow-320\le k\le321\) \(\Rightarrow\) pt có 642 nghiệm
22.
\(sin\left(3x-\frac{\pi}{4}\right)=\frac{\sqrt{3}}{2}\)
\(\Rightarrow\left[{}\begin{matrix}3x-\frac{\pi}{4}=\frac{\pi}{3}+k2\pi\\3x-\frac{\pi}{4}=\frac{2\pi}{3}+k2\pi\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=\frac{7\pi}{36}+\frac{k2\pi}{3}\\x=\frac{11\pi}{36}+\frac{k2\pi}{3}\end{matrix}\right.\)
\(\Rightarrow\) Nghiệm âm lớn nhất \(x=-\frac{13\pi}{36}\) ; nghiệm dương nhỏ nhất \(x=\frac{7\pi}{36}\)
Tổng 2 nghiệm: \(-\frac{13\pi}{36}+\frac{7\pi}{36}=-\frac{\pi}{6}\)
SL
16 tháng 5 2017
ờ,,,,hắn là lớp 9,,,
tui quên ccoong thức bậc 3 r,,,,đợi xem lại tý
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 1
\(\Leftrightarrow\left(sin^2x+cos^2x\right)^2-2sin^2x.cos^2x+\dfrac{1}{2}sin\left(4x-\dfrac{\pi}{2}\right)+\dfrac{1}{2}sin2x-\dfrac{3}{2}=0\)
\(\Leftrightarrow1-\dfrac{1}{2}sin^22x-\dfrac{1}{2}cos4x+\dfrac{1}{2}sin2x-\dfrac{3}{2}=0\)
\(\Leftrightarrow1-\dfrac{1}{2}\left(\dfrac{1-cos4x}{2}\right)-\dfrac{1}{2}cos4x+\dfrac{1}{2}sin2x-\dfrac{3}{2}=0\)
\(\Leftrightarrow-\dfrac{3}{4}-\dfrac{1}{4}cos4x+\dfrac{1}{2}sin2x=0\)
\(\Leftrightarrow-\dfrac{3}{4}-\dfrac{1}{4}\left(1-2sin^22x\right)+\dfrac{1}{2}sin2x=0\)
\(\Leftrightarrow...\)
30 tháng 6 2021
a)Đặt \(t=sinx+cosx\);\(t\in\left[-\sqrt{2};\sqrt{2}\right]\)
\(\Leftrightarrow t^2=sin^2+2sinx.cosx+cos^2x\)
\(\Leftrightarrow t^2=1+2sinx.cosx\)
\(\Leftrightarrow\dfrac{t^2-1}{2}=sinx.cosx\)
Pttt: \(3t-4.\dfrac{t^2-1}{2}=0\) \(\Leftrightarrow-2t^2+3t+2=0\)
\(\Leftrightarrow\left[{}\begin{matrix}t=2\left(ktm\right)\\t=-\dfrac{1}{2}\left(tm\right)\end{matrix}\right.\)
\(\Rightarrow sinx.cosx=-\dfrac{3}{8}\) \(\Leftrightarrow2sinx.cosx=-\dfrac{3}{4}\)\(\Leftrightarrow sin2x=-\dfrac{3}{4}\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{2}.arc.sin\left(-\dfrac{3}{4}\right)+k\pi\\x=\dfrac{\pi}{2}-\dfrac{1}{2}.arc.sin\left(-\dfrac{3}{4}\right)+k\pi\end{matrix}\right.\), \(k\in Z\)
Vậy...
b)Pt
Đặt \(t=sinx-cosx;t\in\left[-\sqrt{2};\sqrt{2}\right]\)
\(\Leftrightarrow t^2-1=-2sinx.cosx\)
Pttt:\(12t+t^2-1=2\)
\(\Leftrightarrow\left[{}\begin{matrix}t=-6+\sqrt{39}\left(tm\right)\\t=-6-\sqrt{39}\left(ktm\right)\end{matrix}\right.\)
\(\Rightarrow cosx+sinx=-6+\sqrt{39}\)
\(\Leftrightarrow\sqrt{2}.cos\left(x-\dfrac{\pi}{4}\right)=-6+\sqrt{39}\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{4}+arc.cos\left(\dfrac{-6+\sqrt{39}}{\sqrt{2}}\right)+k2\pi\\x=\dfrac{\pi}{4}-arc.cos\left(\dfrac{-6+\sqrt{39}}{2}\right)+k2\pi\end{matrix}\right.\)\(,k\in Z\)
Vậy...(Nghiệm xấu)
NV
Nguyễn Việt Lâm
Giáo viên
28 tháng 6 2021
1.
ĐKXĐ: \(x\ne k\pi\)
\(\Leftrightarrow\left(2cos2x-1\right)\left(sinx-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos2x=\dfrac{1}{2}\\sinx=3>1\left(ktm\right)\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=\dfrac{\pi}{3}+k2\pi\\2x=-\dfrac{\pi}{3}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{6}+k\pi\\x=-\dfrac{\pi}{6}+k\pi\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
28 tháng 6 2021
2. Bạn kiểm tra lại đề, pt này về cơ bản ko giải được.
3.
ĐKXĐ: \(x\ne\dfrac{k\pi}{2}\)
\(\dfrac{3\left(sinx+\dfrac{sinx}{cosx}\right)}{\dfrac{sinx}{cosx}-sinx}-2cosx=2\)
\(\Leftrightarrow\dfrac{3\left(1+cosx\right)}{1-cosx}+2\left(1+cosx\right)=0\)
\(\Leftrightarrow\left(1+cosx\right)\left(\dfrac{3}{1-cosx}+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=-1\left(loại\right)\\cosx=\dfrac{5}{2}\left(loại\right)\end{matrix}\right.\)
Vậy pt đã cho vô nghiệm
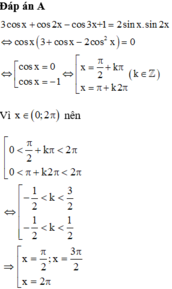
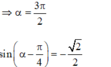
Nhận thấy \(cosx=0\) ko phải nghiệm, chia2 vế cho \(cos^3x\)
\(4tan^3x-\frac{tanx}{cos^2x}-\frac{1}{cos^2x}=0\)
\(\Leftrightarrow4tan^3x-tanx\left(1+tan^2x\right)-\left(1+tan^2x\right)=0\)
\(\Leftrightarrow3tan^3x-tan^2x-tanx-1=0\)
\(\Leftrightarrow\left(tanx-1\right)\left(3tan^2x+2tanx+1\right)=0\)
\(\Leftrightarrow tanx=1\Rightarrow x=\frac{\pi}{4}+k\pi\)
Hai nghiệm âm lớn nhất là \(x=\left\{-\frac{3\pi}{4};-\frac{7\pi}{4}\right\}\) có tổng là \(-\frac{5\pi}{2}\)