cho y=(2x+1)/(x-1) có (C). biết m=m0 là giá trị để (C) cắt d:y=mx+m-1 tại 2 điểm A,B sao cho OAB là tam giác có trọng tâm thuộc d1:x+y-2=0 . giá trị gần m0 là
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
8 tháng 1 2017
Đáp án A.
Xét phương trình hoành độ giao điểm của (C) và (d):
CM
3 tháng 11 2019
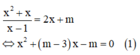
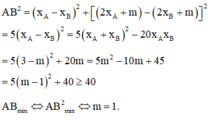
Đáp án B
Hàm bậc 4 trùng phương có ba điểm cực trị ⇒ a b < 0 ⇒ 9 m − 4 < 0 ⇔ m − 4 < 0 ⇔ m < 4
Áp dụng công thức giải nhanh ba điểm cực trị tạo thành tam giác đều thì:
24 a + b 3 = 0 ⇔ 24.9 + m − 4 3 = 0 ⇔ m = − 2
Vậy giá trị m 0 gần giá trị -1 nhất
CM
23 tháng 8 2017
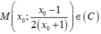- Gọi 
với 
là điểm cần tìm.
- Gọi ∆ tiếp tuyến của (C) tại M ta có phương trình.
- Gọi 
- Khi đó ∆ tạo với hai trục tọa độ tam giác OAB có trọng tâm là
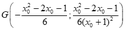
- Do G thuộc đường thẳng 4x+y=0 nên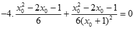 
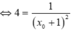(vì A; B không trùng O nên 
)
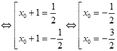
- Vì x0>-1 nên chỉ chọn 
Chọn A.
CM
24 tháng 2 2019
Chọn D.
Phương pháp:
Giải phương trình hoành độ giao điểm, tìm giao điểm của hai đồ thị.
Dựa vào công thức trọng tâm, xác định m.
Cách giải:
Phương trình hoành độ giao điểm của d và (C) là
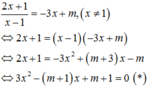
Để d cắt (C) tại hai điểm phân biệt A, B thì (*) có 2 nghiệm phân biệt khác 1
CM
19 tháng 3 2019
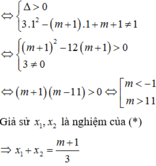
Đáp án D
Phương trình hoành độ giao điểm của C và d là
x x − 1 = m − x ⇔ x ≠ 1 x 2 − m x + m = 0 * .
Để C cắt d tại hai điểm phân biệt ⇔ * có hai nghiệm phân biệt khác 1 ⇔ m > 4 m < 0 .
Khi đó, gọi điểm A x 1 ; m − x 1 và B x 2 ; m − x 2 là giao điểm của đồ thị C và d .
⇒ O A = 2 x 1 2 − 2 m . x 1 + m 2 = 2 x 1 2 − m x 1 + m + m 2 − 2 m = m 2 − 2 m O B = 2 x 2 2 − 2 m . x 2 + m 2 = 2 x 2 2 − m x 2 + m + m 2 − 2 m = m 2 − 2 m
Khoảng cách từ O đến AB bằng
h = d O ; d = m 2 ⇒ S Δ A B C = 1 2 . h . A B = m 2 2 . A B
Ta có
S Δ A B C = a b c 4 R ⇔ R = a b c 4. S Δ A B C = O A . O B . A B 2. h . A B = O A . O B 2. h ⇔ 4 2 . m 2 = O A . O B ⇔ O A 2 . O B 2 = 16 m 2
Khi đó m 2 − 2 m 2 = 16 m 2 ⇔ m 2 − 2 m = 4 m m 2 − 2 m = − 4 m ⇔ m = 0 m = − 2 m = 6 .
Kết hợp với điều kiện m > 4 m < 0 , ta được m = − 2 m = 6 là giá trị cần tìm
CM
31 tháng 12 2019
Đáp án B.
Phương trình hoành độ giao điểm của (C) và d : x − 2 x − 1 = − x + m
⇔ x ≠ 1 x − 2 = ( − x + m ) ( x − 1 ) ⇔ x ≠ 1 f ( x ) = x 2 − m x + m − 2 = 0 ( * )
Để (C) và d cắt nhau tại hai điểm phân biệt A, B khi và chỉ khi phương trình (*) có hai nghiệm phân biệt x 1 , x 2 khác 1
⇔ f ( 1 ) = 1 2 − m + m − 2 ≠ 0 Δ = - m 2 − 4 ( m − 2 ) > 0 ⇔ − 1 ≠ 0 m 2 − 4 m + 8 m > 0 ⇔ m ∈ ℝ .
Mặt khác OAB là tam giác nên O ∈ d hay m ≠ 0 .
Gọi A ( x 1 ; − x 1 + m ) và B ( x 2 ; − x 2 + m ) . Suy ra O A = 2 x 1 2 − 2 m x 1 + m 2 O B = 2 x 2 2 − 2 m x 2 + m 2
Do x 1 , x 2 là hai nghiệm của phương trình (*) nên x 1 2 − m x 1 = 2 − m x 2 2 − m x 2 = 2 − m
Khi đó O A = 2 ( 2 − m ) + m 2 = m 2 − 2 m + 4 O B = 2 ( 2 − m ) + m 2 = m 2 − 2 m + 4
Từ giả thiết ta có :
2 m 2 − 2 m + 4 = 1 ⇔ m 2 − 2 m + 4 = 2 ⇔ m ( m − 2 ) = 0 ⇔ m = 0 m = 2
Đối chiếu với điều kiện ta được m=2 thỏa mãn.
